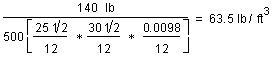The Rural Technology Initiative ceased operations in 2011. This site is maintained as an archive of works from RTI collaborators from 2000 to 2011 and is no longer updated. RTI's successor and remaining staff can be found at NRSIG.org


     
 
   
Search the RTI Website
  
Click to go to the Precision Forestry Cooperative website
Click to go to the RTI Home page
Click to go to the About RTI page
Click to go to the RTI Projects page
Click to go to the RTI Publications page
Click to go to the RTI Tools page
Click to go to the RTI Geographic Information Systems page
Click to go to the RTI Streaming Video Directory
Click to go to the RTI Training page
Click to go to the RTI Contacts page
Click to go to the RTI Image Archive
Click to go to the RTI Site Map
Click to go to the RTI Links page


Chapter 8.  Pulp and Paper


Pulp Yield 

      Mechanical Pulping  

      Chemical Pulping  

             •Kraft (sulfate) process

             •Sulfite process

      Hybrid Pulping Methods

      Dissolving Pulp   

Estimating Wood Required per Ton of Pulp   

Paper and Paperboard

      Basis Weight and Grammage 

             •Basis weight

             •Grammage

      Thickness (Caliper)

      Density and Bulk



Chapter 8.  Pulp and Paper

        Pulp is the fibrous mass that results when a pulping process ruptures the bonds in the wood structure that hold the woody cells together. Pulping is done mechanically, thermomechani­cally, chemically, or with combinations of these treatments. Commercial processes are generally classified as mechanical, chemical, or semi­chemical-the latter being various combinationsof chemical and mechanical. Appendix 2, Section G,  shows that 82% of 1986 production was chemical pulping, of which 91% is produced by the kraft (sulfate) process. Semichemical pulping accounts for about 7% of production, and various mechanical pulping processes account for the remainder.

Pulp statistics are usually reported in units of weight. The most common are

short ton  =  2,000 lb  =  907 kg  

metric tonne  =  1,000 kg  =  2,204 lb.

 Pulp is generally reported as an air-dried product that is assumed to be 10% water and 90% oven-dry pulp. The actual condition of a shipment may vary somewhat from this definition. Pulp is commonly sold in bales (32 x 32 x 15 inches) which weigh about 500 pounds.

Pulp Yield

        Recovery from pulping wood is commonly expressed as the percentage, by oven-dry weight,  of pulp obtained from the original wood weight. A recovery value of 45% means that for every 100 oven-dry pounds of wood processed, 45 oven-dry pounds of pulp is produced. When expressed in this manner, pulp yield is mainly a function of the pulp­ing process. There is some difference between hard­woods and softwoods when pulped by chemical processes, due to the difference in chemical makeup between these groups. Table 8-1provides a summary of common pulping processes and yields. Section G of Appendix 2 shows percentage use of hardwood and softwood species.

Mechanical Pulping

        The earliest and one of the most common mechanical pulping methods is the groundwood process, in which a roundwood bolt is pressed lengthwise against a rough, revolving grinding stone. The wood fibers are torn out of the wood, abraded, and removed from the stone surface with water. A different process, called refiner mechan- ical pulp (RMP) utilizes chips, which are shredded into fibers between large rotating disks of a device called a refiner. The basic RMP process has evolved to employ thermal and/or chemical presoftening of the chips, which reduces energy use and modifies resultant pulp properties; this is typically termed thermomechanical pulp (TMP). Mechanical pulping has the advantage of converting up to 95% of the dry weight of the wood input into pulp, but the mechanical action requires a large energy input. The pulp forms a highly opaque paper with good printing properties, but the paper is relatively weak and discolors easily with exposure to light. Newsprint is a major product of mechanical pulp. Mechanical pulps are generally produced from long-fibered softwood (conifer) species. The smaller, thinner fibers from hard­woods are more severely damaged by the mechan­ical action, hence yield a weaker paper. However, some hardwoods, such as poplar, which produces very bright pulp, are mechanically pulped and blended with softwood mechanical pulps to improve optical properties.

Chemical Pulping

        In chemical pulping, the fibers in wood are separated by dissolving away the lignin com-ponent, leaving behind a fiber that retains most of its cellulose and some hemicellulose. Yields of chemical processes are on the order of 40 to 50% of the dry weight of the original wood input.

Kraft (Sulfate) Process.     Because of advantages in chemical recovery and pulp strength, the kraft process dominates the industry. It represents 91% of chemical pulping and 75% of all pulp (Appendix 2, Section G). It evolved from an earlier soda process (using only sodium hydroxide as the active chem-ical) and adds sodium sulfide to the cooking chemical formulation. This is the process asso­ciated with the foul odor problem in the environ­ment. A number of pulp grades are commonly produced, and the yield depends on the grade of product. Unbleached pulp grades, characterized by a dark brown color, are generally used for packaging products and are cooked to a higher yield and retain more of the original lignin. Bleached pulp grades are made into white papers. Figure 8-1 shows a pulping curve and relationship between yield, kappa number, and corresponding product. Nearly half of the kraft production is in bleached grades, which have the lowest yields. In Figure 8-1, kappa number refers to the result of a test of the amount of residual lignin in the pulp-lower kappa meaning less lignin. Effective alkali and sulfidity refer to conditions of certain key chemical aspects of the process (for details see Smook 1992). Curves such as shown in Figure 8-1 also differ with wood species.

Figure 8-1.  Kraft pulp yield vs. kappa and effective alkali charge. Source: Smook (1992).  
Sulfite Process.     This process uses different chemicals to attack and remove lignin. Compared to kraft pulps, sulfite pulps are brighter and bleach more easily, but are weaker. Sulfite pulps are produced in several grades but bleached grades dominate production. Yields are generally in the range of 40 to 50%, but tend toward the lower end of this range in bleached grades. Compared to the kraft process, this operation has the disadvantage of being more sensitive to species characteristics. The sulfite process is usually intolerant of resinous softwoods, tannin-containing hardwoods, and any furnish containing bark.

Hybrid Pulping Methods

        A number of processes are hybrids of chemical and mechanical methods and have intermediate yields. Generally, chips are partly softened or digested with chemicals and then are mechan­ically converted to fiber, usually in disk refiners. Chemimechanical pulping, typically used on hardwoods, softens chips prior to usual mechanical action and has yields in the 80 to 90% range. Semi­chemical pulping involves greater cooking and delignification prior to mechanical refining; yields are somewhat lower, depending on the degree of cooking.

Dissolving Pulp

        Dissolving pulps are specialty pulps used for chemical conversion into products such as rayon, cellophane, and cellulose acetate. These pulps can be made by either a modified kraft (prehydrolysis) or sulfite process in which the aim is to obtain a pulp of pure cellulose. Since essentially all lignin and hemicellulose are removed, dissolving pulps have the lowest yields, on the order of 35%.

Estimating Wood Required per Ton of Pulp

        It is also common to express pulp yield as air-dry or oven-dry tons of pulp per cord or other unit of wood volume. Alternatively, the reciprocal of these measures indicates the number of cords or other wood unit required per ton of pulp. In addition to the factors discussed above, these measures are affected by wood density. Yield is generally higher (less wood is required) for denser species. To estimate wood required per ton of pulp, the following information is needed: (1) moisture content of pulp, (2) pulp yield, and (3) specific gravity of the species used as raw material. There are several variations in calculating wood requirements, due to the different measures of pulp (short ton, metric tonne) and different measures for the wood raw material (cubic foot, cubic meter, bone-dry unit). A bone-dry unit (BDU) represents 2,400 pounds of chips or residues. See Chapter 7 for further discussion of chip and residue measures and conversions. Basic formulas are:

Formula 1.  MCw = [(WP - DP) / WP] * 100

        MCw  =     pulp moisture content on total
                          weight basis (%)

        WP  =  pulp weight including moisture

        DP  =  oven-dry weight of pulp

Formula 2.  Y  =  (DP / DW) * 100

        Y  =  pulp yield (%)

        DW  =  oven-dry weight, wood raw material

Formula 3.  DW  =  V  *   SGg  *   F

        V  =  green volume of wood raw material

        SGg  =  wood specific gravity (see Table 1-1)

        F  =   density of water  =  62.4 lb/ft3  or 
                           1,000 kg/m3

        In Examples 1 through 7 the pulp moisture content is assumed to be 10%. These examples illustrate both the information needed and computational steps involved in developing the common conversion factors of interest. The reader can substitute yields for other processes, specific gravities for other species, and other pulp moisture contents. Appendix 2, Section G,  presents overall average values of wood consumption in manu­facturing pulp in 1986. It should also be noted that about 31% of the solid pulpwood used is actually in the form of residue by-products from other wood industries (Haynes 1990).

Example  1

How many cubic feet of solid western hemlock wood are needed to produce one short ton (2,000 lb) of oven-dry bleached kraft pulp (kappa 30)?

Formula 1 gives  10  =  [(2,000 lb - DP) / 2,000 lb] * 100
solving: DP = 1,800 lb of oven-dry fiber per ton of pulp.

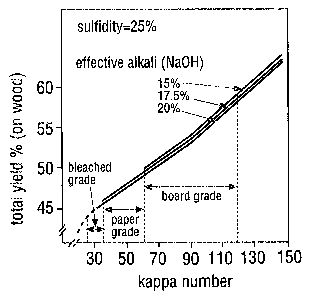
Formula 2 gives  45  =  (1,800 lb / DW) * 100
solving: DW  =  4,000 lb oven-dry wood per ton of pulp.

      Here the yield of bleached kraft pulp is assumed to be 45% (Figure 8-1).

Formula 3 gives  4,000 lb = V * 0.42 * 62.4 lb/ft3
solving: V = 153 cubic feet of green wood per ton of pulp.
Here 0.42 is the specific gravity of western hemlock
(Table 1-1).

Example   2

How many cubic meters of solid western hemlock wood are needed to produce one tonne (1,000 kg) of oven-dry bleached kraft pulp (kappa 30)?

Formula 1 gives  10  =  [(1,000 kg - DP) / 1,000 kg] * 100
solving: DP = 900 kg of oven-dry fiber per tonne of pulp.

Formula 2 gives  45  =  (900 kg / DW)  * 100
solving: DW  =  2,000 kg oven-dry wood per tonne of pulp.
Here the yield of bleached kraft pulp is assumed to be 45% (Figure 8-1).

Formula 3 gives  2,000 kg = V * 0.42 * 1,000 kg/m3
solving: V  =  4.76 cubic meters of green wood per tonne of pulp.
Here 0.45 is the specific gravity of western hemlock (Table 1-1).

Example  3

How many cords of western hemlock wood are needed to produce one short ton of oven-dry bleached kraft pulp?

Example 1 found that 153 cubic feetof solid green wood  are needed per ton of bleached Douglas-fir kraft pulp. Assuming a cord contains 80 cubic feet of solid wood (Chapter 3), this is equivalent to 1.91 cords/ton.

Example  4

How many cubic feet of gravity-packed western hemlock chips are needed to produce one short ton (2,000 lb) of oven-dry bleached kraft pulp?

To answer this question, one must know the relationship between wood volume before and after chipping. This depends on chip geometry, degree of settling and compaction, and so forth, which are discussed in Chapter 7. In this example it is assumed that chips occupy 2.5 times the original solid wood volume (see Table 7-1). Example 1 found that 153 cubic feet of solid western hemlock wood were needed to produce a ton of pulp. The equivalent amount of chips is 2.5 times greater, or 382.5 cubic feet.

Example  5

How many "units" of western hemlock chips are needed to produce a ton of oven-dry bleached kraft pulp?

A "unit" typically refers to a 200 cubic foot container. Example 4 found that a ton of bleached kraft pulp requires 382.5 cubic feet of western hemlock chips. Division by 200 reveals that this is equivalent to 1.91 units.

Example  6

How many bone-dry units (BDU) of chips are needed to produce an oven-dry ton of pulp?

Example 1 found that 4,000 pounds of oven-dry wood are needed per ton of pulp. Since one BDU equals 2,400 pounds of oven-dry wood, the answer is

      (4,000 lb/ton pulp) / (2,400 lb/BDU)  =  1.67 BDU/ton pulp.

Example  7

How many bone-dry units (BDU) are needed to produce an oven-dry tonne of pulp?

Multiply the result from Example 6 by

        (2,204 lb/tonne) / (2,000 lb/ton)  =  1.102 ton/tonne.

Hence, 1.67 BDU/ton * 1.102 ton/tonne  =  1.84 BDU/tonne.


Paper and Paperboard

        When paper and paperboard are produced, converted, and sold, several measurements are important. This section briefly discusses them and provides some illustrative data. Industry statistics are usually reported on a weight basis, and the standard weight conversions found in Appendix 1 can be used.

Basis Weight and Grammage

        When paper and paperboard are produced and converted, two key characteristics are weight and area. Production is generally reported in tons, and products are sold on either a weight or an area basis depending on the needs of the customer.

Basis Weight.     The common measure in the United States, basis weight,is"the weight, in pounds, of a predetermined number of sheets having a specific size" (Scott 1989). The predetermined number of sheets is the ream. Generally 500 sheets form a ream, but a ream contains 480 sheets for some pro­ducts. Since various producers and converters need different size sheets, a variety of basic sizes have evolved over time. Table 8-2 indicates basic size and basis weights for several grades (500 sheet ream). For example, cover papers have basis weights of 40, 50, 60, 65, 70, 80, 100, and 130; all are based on a 500 sheet ream of 20 by 26 inch sheets. Unfortunately, these basic sizes have no common relationship; hence, conversions among them require knowledge of actual sheet size and number of sheets involved. Essentially, the calculations require prorating the actual size and number of sheets to the standard basis size for the grade and to the number of sheets in a ream. Saltman (1991) provides a number of illustrative practical examples. To further complicate matters, the U.S. Government Printing Office uses a unit of 100 sheets, and basis weight for paperboards is usually given as pounds per 1,000 square feet. The U.S. system is very cumbersome and can lead to confusion and misunderstanding. Grammage, as defined below, is gaining popularity, since it is simpler and is widely used internationally.

Grammage.     In the SI or metric system, basis weight is called grammage, which is the weight in grams per square meter (Scott 1989). This definition eliminates confusion caused by different standard sizes and different ream counts. Table 8-2 shows how basis weights of various grades relate when expressed in grammage. In the U.S. system, book and cover papers both have a basis weight of 50 within the range for each of these grades. Table 8-2 shows that the grammages are 74 and 135, respectively. This difference was masked by the U.S. practice of measuring basis weights on 25 by 38 inch and 20 by 26 inch areas, respectively. Table 8-3 provides factors for converting basis weights.

Thickness (Caliper)

        Thickness is an important determinant of stiffness. In addition, paper thickness determines overall thickness of finished products such as books, and hence the space they will occupy. In the United States, thickness is in inches, with the terms point and mil used to refer to thousandths of an inch. In the SI or metric system, thickness is in micrometers. Table 8-4 presents comparable thickness measures for several paper grades.

Density and Bulk

        Two additional properties of interest are density and bulk. Apparent density, in grams per cubic centimeter, is obtained by dividing grammage by thickness. Density in grams per cubic centimeter (g/cc) can be converted to pounds per cubic foot (lb/ft3)bymultiplying by 62.4. Density influences most physical, mechanical, and other properties. Bulk is the reciprocal of density. It measures the volume in cubic centimeters (cc) occupied by one gram of paper or the volume in cubic feet occupied by one pound of paper. See Example 8.


Example  8

Tables 8-2 and 8-4 indicate that index bristol, with gram­mage of 253 g/m2 (basis weight 140 lb), has a thickness of 0.25 mm (0.0098 inch).  Density, g/cc  =  253  g/m2 /(1,000 * 0.25 mm)  = 1.012 g/cc.(The number 1,000 results from 1 m2 =  10,000 cm2 and 1 cm  =  10 mm.)  Density, lb/ft3  =  1.012    62.4  =  63.2 lb/ft3

                                        or

 

        Bulk, cc/g  =  1/1.012  =  0.988  cc space per gram.        Bulk, ft3/lb  =  1/63.2  =  0.016 ft3 space per pound.


Table 8-2. Examples of basis weight and grammage for several grades of paper, based on a 500 sheet ream
(basic sheet size in parentheses).

Basis weight (lb)
Bond, ledger,
mimeo, writing (17 x 22)
Cover(20 x 26)		 Postcard,
wedding bristol
(22-1/2 x 28-1/2)
Index bristol
(25-1/2 x 30-1/2)		 Glassine, news,
tissues, wrapping
(24 x 36)		 Book, bible,
offset, blotting
(25 x 38)		 Grammage
(g/m2)
x       x 20 30
9       x x 34
x       x 24 36
11       x x 41
x       x 30 44
             
13       30 33 49
x       x 35 52
15       x x 56
x       x 40 59
16       x x 60
             
x       40 x 65
x       x 45 67
x       x 50 74
20       x x 75
x       50 x 81
             
x       x 60 89
24       x x 90
x       60 x 98
x       x 70 104
28       x x 105
             
x 40     x x 108
x x     70 x 114
x x     x 80 118
32 x     x x 120
x x     80 x 130
             
x x x   x 90 133
36 50 x   x x 135
x x x   90 x 146
x x 67   x x 147
x x x   x 100 148
             
40 x x x x x 150
x 60 x x x x 162
x x x 90 100 x 163
x x 80 x x x 175
x 65 x x x x 176
             
  x x x x 120 178
  70 x x x x 189
  x 90 x x x 197
  x x 110 x x 199
  x x x 125 x 203
             
  80 x x x   216
  x x x x   218
  x 100 x x   219
  x x x 150   244
  x x 140 x   253
             
  x x x x   262
  x 120 x x   263
  100 x x x   270
  x x x 175   285
  x x x x   306
             
  x 140 170 x   307
  x x x 200   325
  x x x x   349
  x 160 x x   351
  130 x x x   352
             
    180 x x   395
    x 220 x   398
    x x 250   407
    200 x     438

Sources:  Adapted from Saltman (1991) and Scott (1989).


Table 8-3.  Factors for converting basis weights from one basic size to another.

Convert to:

g/m2

17 x 22-500

24 x 36-500

25 x 38-500

25 x 40-500

1,000 ft2

Actual ft2

  
               

Convert from:

1.000

0.266

0.614

0.676

0.711

0.205

-

g/m2

              

17 x 22 - 500

3.759

1.000

2.311

2.541

2.675

0.770

1,300

24 x 36 - 500

1.627

0.451

1.000

1.100

1.158

0.333

3,000

25 x 38 - 500

1.480

0.394

0.909

1.000

1.052

0.303

3,300

25 x 40 - 500

1.406

0.374

0.864

0.950

1.000

0.288

3,470

1,000 ft2

4.882

1.299

3.000

3.298

3.472

1.000

1,000
 

Source: Scott (1989).

Example: To convert from 60 lb of size (25 x 40-500) to weight of basic size (17 x 22-500) look up the multiplying factor associated with (25 x 40-500) in the "Convert from" column and (17 x 22-500) in the "Convert to" row. The new basis weight is calculated as follows:

60 lb (25 x 40-500)  x  0.374  =  22.4 lb (17 x 22-500).

Table 8-4.  Representative thickness values of several grades of paper and board.

 

Paper

mm

Inches

"Points"

Micrometers

  
  Capacitor           0.0076           0.0003               0.3              7.6  
  Glassine           0.03           0.0012               1.2             30  
  Facial tissue           0.065           0.0025               2.5             65  
  Tablet           0.075           0.003               3.0             75  
  Newsprint           0.085           0.0033               3.3             85  
  Duplicator           0.095           0.0037               3.7             95  
  Rag bond           0.11           0.0043               4.3             110  
  Kraft envelope           0.13           0.0051               5.1             130  
  Index bristol           0.25           0.0098               9.8             250  
  Corrugating medium           0.23           0.009               9.0             230  
  Linerboard           0.23-0.64           0.009-0.025               9-25             230-640  
  Chipboard           0.15-0.41           0.006-0.016               6-16             150-410  
  Cardboard blanks           0.30-2.0           0.012-0.0780               12-78             300-2,000  

Source: Scott (1989).
 
School of Environmental and Forest Sciences
USDA Forest Service State & Private Forestry
WSU Cooperative Extension
The Rural Technology Home Page is provided by the College of Forest Resources. For more information, please contact the Rural Technology Initiative, University of Washington Box 352100 Seattle, WA 98195, (206) 543-0827. © 2000-2004, University of Washington, Rural Technology Initiative, including all photographs and images unless otherwise noted. To view the www.ruraltech.org privacy policy, click here.
Last Updated 10/13/2022 12:34:06 PM