|
 |
 |
 |


Measuring the impact of harvest intensity
on riparian forest functionality in terms of shade production and large
woody debris recruitment potential: two models.
|
Jason Cross
A thesis submitted in partial fulfillment of the requirements for the degree of
Master of Science
University of Washington
Program Authorized to Offer Degree:
|
| Figure 1 | Shade Model Construction Step 1 |
| Figure 2 | Shade Model Construction Step 2 |
| Figure 3 | Shade Model Construction Step 3 |
| Figure 4 | Shade Model Construction Step 4 |
| Figure 5 | Shade Model Construction Step 5 |
| Figure 6 | Shade Model Construction Step 6 |
| Figure 7 | Shade Model Construction Step 7 |
| Figure 8 | Shade Model Construction Step 8 |
| Figure 9 | Shade Model Construction Step 9 |
| Figure 10 | Shade Model Construction Step 10 |
| Figure 11 | Shade Model Construction Step 11 |
| Figure 12 | LWD Model Construction Step 1 |
| Figure 13 | LWD Model Construction Step 2 |
| Figure 14 | LWD Model Construction Step 3 |
| Figure 15 | LWD Model Construction Step 4 |
| Figure 16 | LWD Model Construction Step 5 |
| Figure 17 | Stand Visualization - MR_SHELTERWD |
| Figure 18 | Stand Visualization - BR_STEEPLES |
| Figure 19 | Stand Visualization - MR_27CR_RMZ |
| Figure 20 | Shade Model Results - Baseline |
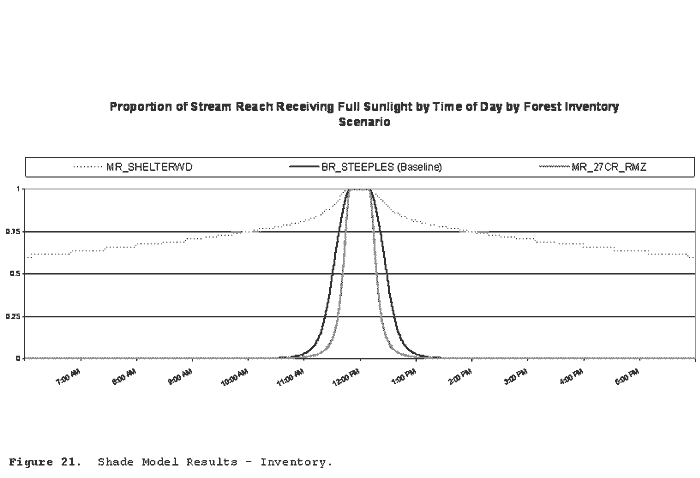
| Figure 21 | Shade Model Results - Inventory |
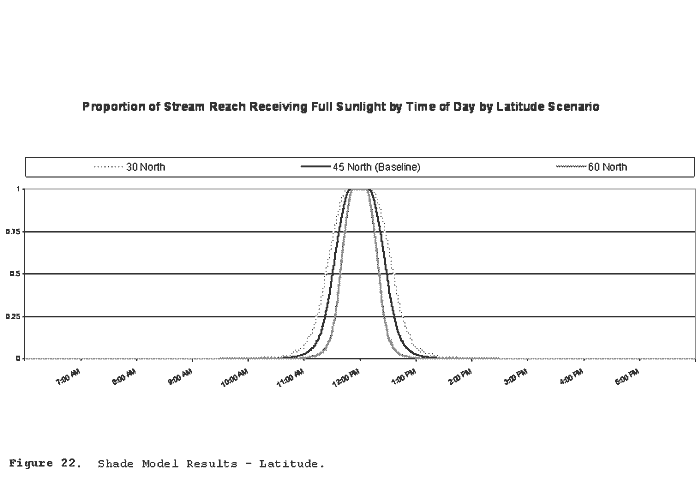
| Figure 22 | Shade Model Results - Latitude |
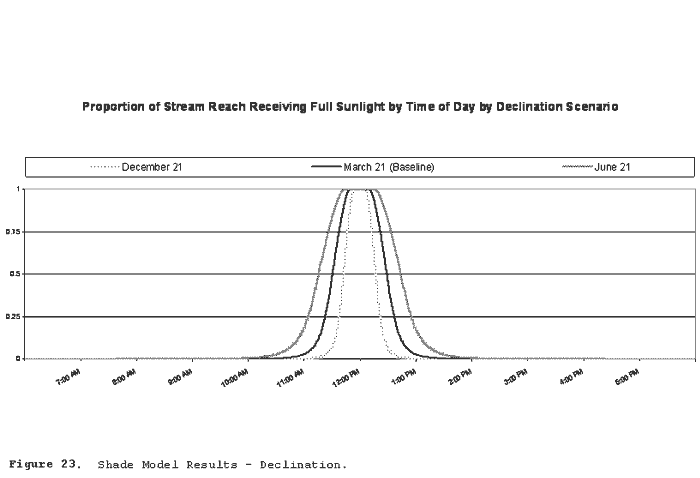
| Figure 23 | Shade Model Results - Declination |
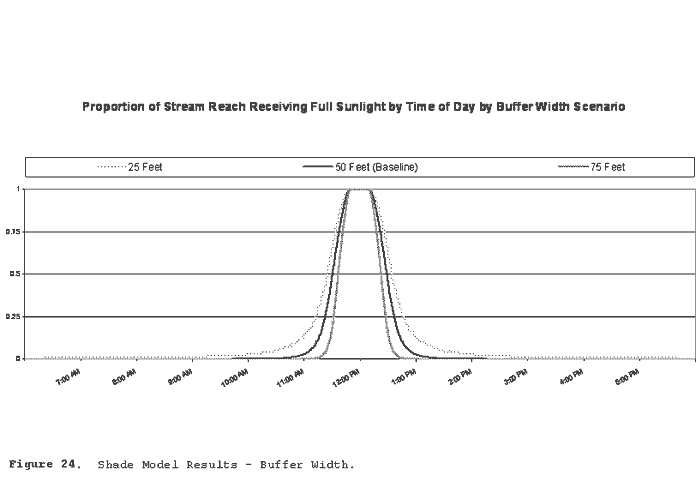
| Figure 24 | Shade Model Results - Buffer Width |
| Figure 25 | Shade Model Results - Buffer Slope |
| Figure 26 | Shade Model Results - Stream Width |
| Figure 27 | Shade Model Results - Stream Reach |
| Figure 28 | Shade Model Results - Stream Gradient |
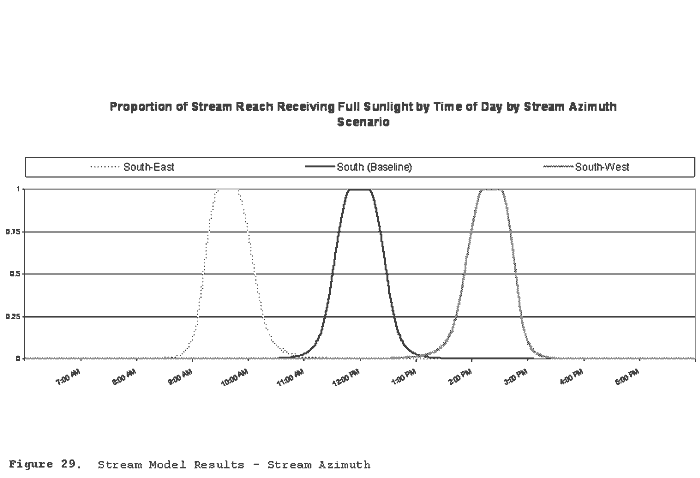
| Figure 29 | Shade Model Results - Stream Azimuth |
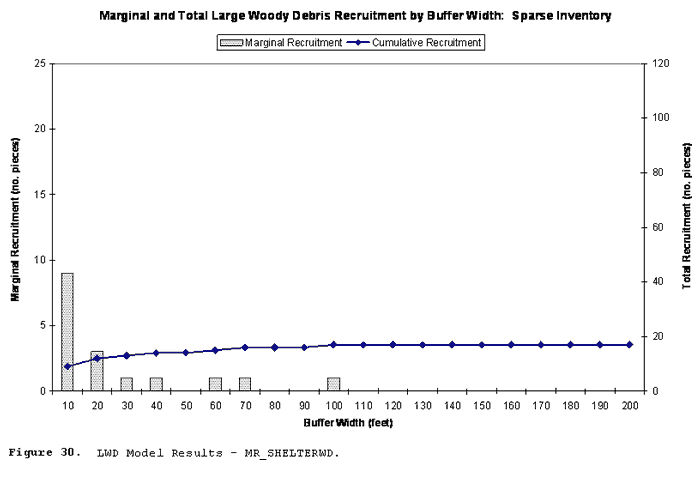
| Figure 30 | LWD Model Results - MR_SHELTERWD |
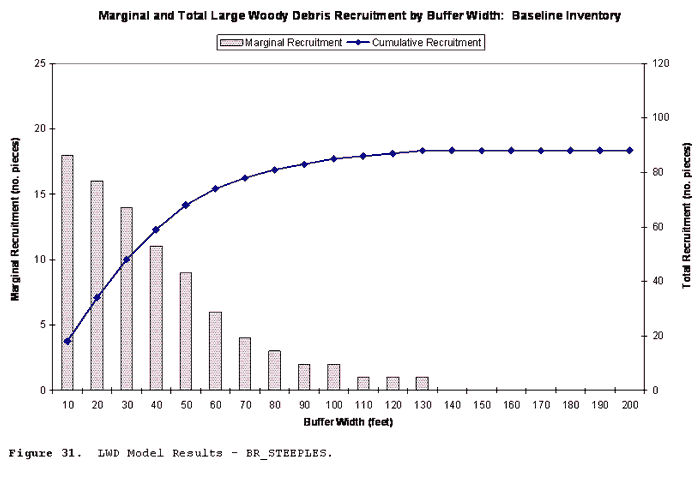
| Figure 31 | LWD Model Results - BR_STEEPLES |
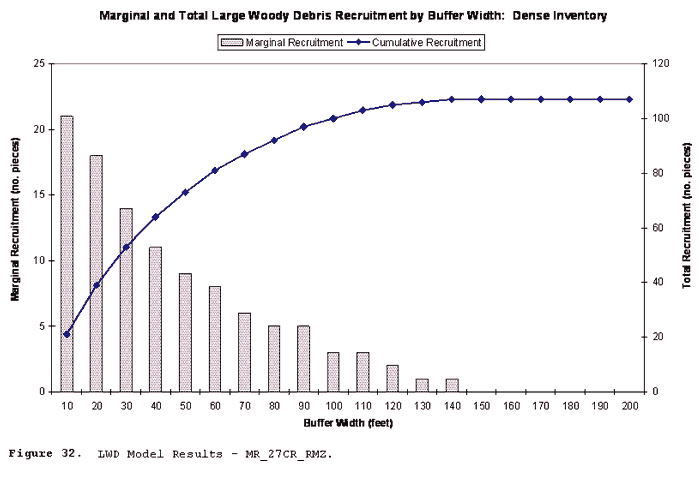
| Figure 32 |
LWD Model Results - MR_27CR_RMZ |
List of Tables
| Table 1 | Shade Analysis Procedures Summary Table |
| Table 2 | Stand Summary Table |
| Table 3 | Shade Analysis Results Summary Table |
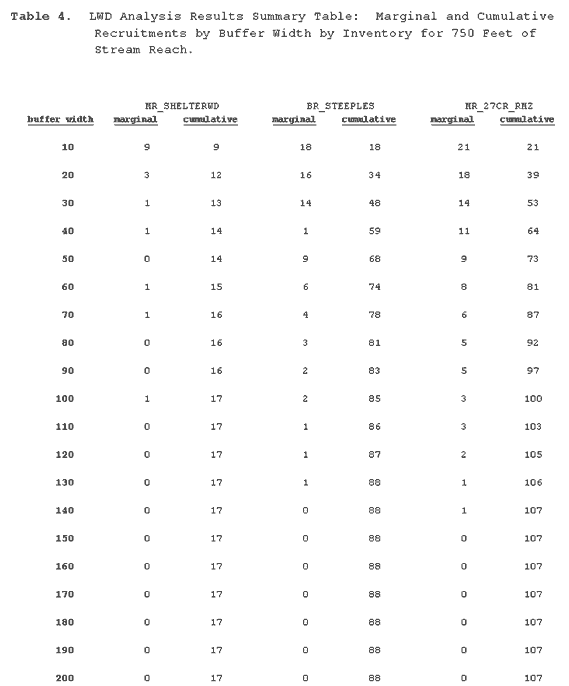
| Table 4 | LWD Analysis Results Summary Table |
Introduction
Considerable attention - both in theory and policy - has been devoted to the management of riparian forests. Researchers and legislators alike are concerned with the impacts of timber harvest intensity on the functionality of riparian systems - specifically, on the ability of riparian forests to provide and maintain suitable aquatic habitat.
In order to manage riparian forests effectively for these objectives in concert with others, two questions must be answered: "What are the primary and/or unique functions of riparian forests?" and more pointed, "How does timber harvest intensity affect production and maintenance of aquatic habitat?"
Numerous studies - many of them literature reviews on nature - have sought to identify both the essential functions of riparian forests and those specific functions that are necessary for suitable aquatic habitat. Although any given list is likely to be more or less extensive than another, there is general agreement within the body of literature (Castelle et al . 1994; Johnson and Ryba 1992; NCASI 2000) that any such list must include:
-
(1) Shade Production
(2) Large Woody Debris Recruitment (LWD)
(3) Particulate Organic Matter recruitment (POM)
(4) Sediment Reduction
(5) Streambank Stabilization
(6) Chemical Removal
The set of riparian functions that are applicable to the production and maintenance of aquatic habitat is likely to be a subset of those mentioned above. There is further agreement (Barton et al . 1985; Castelle et al . 1994; Johnson and Ryba 1992; NCASI 1999; NCASI 2000; Patton 1974) that the following functions are essential to aquatic habitat:
-
(1) Shade Production
(2) Large Woody Debris Recruitment (LWD)
Different harvest intensities will have different effects in terms of shade production and LWD recruitment on similar sites; similar harvest intensities applied across a variety of sites will also have different effects. Thus it may be difficult to develop a "rule of thumb" for management prescriptions across riparian forests. The uniqueness of each riparian forest may require individual analysis, necessitating the formulation of tools to analyze the impact of different harvest intensities for a given set of background conditions.
Research Objectives
The present riparian situation is best captured in the writings
of Professor J. Neyman:
-
Whenever we use mathematics in order to study some observational
phenomena we must essentially begin by building a mathematical model
(deterministic or probabilistic) for these phenomena. Of necessity,
the model must simplify matters and certain details must be ignored.
The success or the model depends on whether or not the details ignored
are really unimportant in the development of the phenomena studied.
The solution of the mathematical problem may be correct and yet
be in considerable disagreement with the observed data simply because
the underlying assumptions made are not warranted. It is usually
quite difficult to state with certainty, whether or not a given
mathematical model is adequate before some observational
data are obtained. In order to check the validity of a model, we
must deduce a number of consequences of our model and then compare
these predicted results with observations.
Two observational phenomena critical to the production and maintenance of adequate aquatic habitat were outlined in the introduction: (1) Shade production and (2) large woody debris recruitment.
The purpose of this research is to develop two mathematical models:
A deterministic model for shade production and a probabilistic model for in-stream large woody debris (LWD) recruitment that allow for comparisons of harvest intensity effects between management scenarios.
The shade model will have the following variables:
- Inventory Composition
- Latitude
- Declination
- Buffer Width
- Buffer Slope
- Stream Width
- Stream Reach
- Stream Gradient
- Stream Azimuth
The LWD model will have the following variables:
- Inventory Composition
- Buffer Width
- Buffer Length (stream reach)
Using a trio of forest inventories (taken from the University of
Washington's Pack Forest) a sensitivity analysis will be performed
on both models to analyze the reasonableness of the results.
Literature Review: Shade Production
Adams and Sullivan (1989) asserted that among the most important factors influencing stream heating and cooling are solar insolation (radiation), ambient air temperature, relative humidity, and groundwater influx. These conclusions have been partially or fully supported by the findings of Brown (1969), Byram and Jemison (1943), and NCASI (2000). Substrate composition and stream depth were also found to be significant (Brown, 1969; NCASI, 2000), along with discharge rate (NCASI, 2000; Patton, 1974). The length or reach of the stream is important; it determines the exposure time to the stream (Brazier and Brown, 1973). There is general consensus that these factors combine in a unique fashion for any given stream; that is, the relative importance of any one factor is unpredictable without knowledge of all factors.
Because of the extreme distance of the sun from the earth, solar rays arrive at the earth essentially parallel to one another. Solar radiation reaches a stream either directly or via a diffuse pathway (Ice, 1999; Adams and Sullivan, 1989). Adams and Sullivan (1989) concluded that daily mean stream temperature is always very close to daily mean air temperature when the stream is in equilibrium with its environment (i.e. after initial warming period at sunrise and cooling at sunset). Furthermore, their research concluded that solar radiation (either direct or diffuse) has a relatively small influence on daily mean stream temperature. At the same time, however, fluctuations about the mean daily stream temperature are highly influenced by solar exposure and riparian vegetation.
Concerning riparian vegetation and solar radiation, Barton, Taylor and Biette (1985) confirmed with their research the results of Brown and Krygiers (1970) that the most important cause of high stream temperatures is direct solar radiation resulting from the absence of shading by forest cover. Riparian forest measurements associated with shade production include canopy density, vegetation height, crown radius, aspect and slope (NCASI, 2000). Furthermore, increased direct short-wave solar radiation is the primary energy input that causes elevated stream temperatures (Ice, 1999). Adams and Sullivan (1989) concluded that the only precise method of obtaining solar radiation input to a stream is to measure it for a specific site at a specific time. Ice (1999) commented that crude estimates of potential increases in temperature are possible by only considering change in direct short-wave radiation.
The conclusions of the research above suggest that increased direct solar radiation is the most significant cause of short-term stream temperature increases. Loss of riparian vegetation cover is the principal vehicle for increasing solar insolation upon streams. Canopy density along the path of incoming direct solar radiation best describes the ability of riparian forest vegetation to control stream temperatures (Brazier and Brown, 1973).
There are many methods available for calculating canopy closure (density): view-to-sky, ocular estimation, spherical densiometer. There are drawbacks to these methods because they integrate across all heights to arrive at a single number result. Integrating across all heights necessarily means that you cannot account for the path of an individual incoming ray (Brazier and Brown, 1973; Ice, 1999). Measurements for specific sites at specific times are precisely what are needed (Adams and Sullivan, 1989) to measure direct solar radiation inputs accurately. Measures such as ACD, solar pathfinder, and hemispherical photography do account for the path of incoming radiation; however, employing a solar pathfinder or hemispherical photography is extremely expensive compared to angular canopy densiometers. There is also evidence to suggest that shade produced by riparian forest vegetation is not a reliable estimator of angular canopy density (NCASI, 1999). Regardless of the relationship between ACD and shade, use of densiometers is subjective, imprecise, and inaccurate (Ganey and Block, 1994).
Measuring canopy density or closure along the path of incoming solar radiation requires knowledge of crown closure at (potentially) every level of the canopy. This requires knowledge of crown morphologies and spatial coordinates of trees. Crown morphology is a function of many variables: height, relative dominance, species, density, and more. Most of these measures can only be accurately modeled with a spatially explicit growth model (i.e. a growth model that knows where every tree is in relation to every other tree). Unfortunately, the effort required to obtain the type and amount of data necessary to employ such a model is often cost-prohibitive. Representations of crown shapes range from basic/abstract to extremely detailed: conic sections, parabaloids, eccentric crowns, cylinders, parallelepipeds, and individual leaf representations (Brunner, 1998). The amount of information required to take advantage of progressively complex crown representations exceeds what is known in general or for any given individual stand (Brunner, 1998). Consequently a simplification of a detailed crown model is acceptable given the set of data typically collected from the forest.
Literature Review: Large Woody Debris Recruitment
The role and importance of large woody debris (LWD) in the maintenance
and production of riparian and aquatic habitat was largely misunderstood
for much of the 20th century (Bisson et al
. 1987; Bryant 1983; Harmon et al . 1988; Triska
and Cromack 1979). Many saw large woody debris in the stream channel
as detrimental to stream quality and reforestation efforts (Triska
and Cromack 1979). Riparian forest management practices reflected
such attitudes, and fish-bearing streams were often cleared of all
woody debris during logging operations (Bisson et al .
1987).
Attitudes towards in-stream large woody debris have changed within
the past 20 to 25 years. Studies suggest that large woody debris
plays an integral role in maintenance and production of riparian
and aquatic habitat (Beechie and Sibley 1997; Bisson et al
. 1987; Bryant 1983; Harmon et al . 1988; Swanson et
al . 1977; Swanson and Lienkaemper 1978; Triska and Cromack
1979). Current riparian management practices illustrate this paradigm
shift, so that deleterious impacts on large woody debris recruitment
potential are assessed and mitigated (Murphy and Koski 1989).
If LWD production is an important management objective, then understanding how LWD is recruited (processes and mechanisms), and the effect of changes in temporal and spatial conditions thereon, is necessary to develop a comprehensive management plan (Beechie and Sibley 1997; Spies et al . 1988).
LWD recruitment agents can be classified in one of two categories: biological and physical. Biological agents include natural, insect-induced, and disease-induced mortality (Keller and Swanson 1979). Physical processes that recruit in-stream LWD include windthrow; streambank failure caused by undercutting, mass soil movement; and avalanches of both debris and snow (Keller and Swanson 1979). These processes are not independent of each other and often act in concert to deposit LWD into a stream channel (Bryant 1983; Keller and Swanson 1979; Murphy and Koski 1989; Swanson et al . 1977; Swanson and Lienkaemper 1978). Among these processes, windthrow, streambank failure, and natural mortality account for the majority of in-stream LWD (Bisson et al . 1987; Bryant 1983; Harmon et al . 1988; Keller and Swanson 1979; Murphy and Koski 1989; Swanson et al . 1977; Swanson and Lienkaemper 1978; Triska and Cromack 1979).
Triska and Cromack (1979) suggested that recruitment potential will vary systematically with stand development stage; in unmanaged conditions, recruitment and accumulation must be considered on a temporal scale of 400 - 500 years, the return interval for catastrophic, stand replacing fires in the Pacific Northwest. This assertion is supported in other studies (Spies et al . 1988; Van Sickle and Gregory, 1990) which conclude that LWD input rates are significantly different between young, mature, and old-growth stands.
In addition to temporal variations, LWD recruitment rates will differ with each unique combination of site-specific physical and spatial characteristics (Bisson et al . 1987). Such characteristics include species composition, soil composition, soil stability, valley form, aspect, and management history.
Even the most conducive set of biological, physical, spatial, and temporal characteristics (for the purpose of LWD recruitment) will recruit from only a subset of the total forest inventory. This subset can be considered the set of LWD candidates.
Robison and Beschta (1990) asserted that the probability of a given tree falling into a stream is dictated by the tree's height and its distance from the stream. Specifically, if the probability space of the tree's fall is a circle centered on the tree with radius equal to the tree's height, then the probability of a tree becoming LWD is the proportion of the entire probability space that overlaps the stream (also McDade et al . 1989). If the distance to the stream from a given tree is greater than that tree's height, then its probability of recruitment is zero (Robison and Beschta 1990); the set of LWD candidates is comprised of those tree's whose probability (as described above) is greater than zero. This may be a simplification, since some studies offer evidence that debris slides can deliver LWD to streams (Lienkaemper and Swanson 1986; Murphy and Koski 1989; Swanson and Lienkaemper 1978; Swanson et al . 1977). Van Sickle and Gregory (1990) suggested that, although sliding and rolling may indeed result in significant downslope movement of LWD, it may not add a significant number of new pieces of in-stream LWD from what otherwise are considered non-candidates.
The probability of LWD recruitment is the straight proportion of probability space overlapping the stream if it is assumed that the direction of a tree's fall is random (uniform) to all directions. This may not always be the case, as some studies (Featherton et al . 1995; Lienkaemper and Swanson 1986; McDade et al . 1989; Robison and Beschta 1990; Van Sickle and Gregory 1990) suggest that there are systematic influences in the direction of a tree fall, such as hillslope steepness, soil cohesive properties (especially close to the streambank), and prevailing wind directions. A scarcity of literature on this subject leads to the conclusion that the exact amount of influence exerted by any one factor is debatable.
It is reasonable to begin with an assumption of uniformity in direction
of a tree fall and add or subtract from that probability based on
site specific analysis of how each factor may create an incentive
towards or deterrent from LWD recruitment.
Theoretical Construction: Shade Production
The initial conditions and assumptions for constructing the model
is illustrated in Figure 1: a consistent reach of stream in terms
of azimuth (Z) and width, both of which are known. Simplifying assumptions
such as a straight reach, uniform streambank width, and a flat planar
stream surface are made for this analysis.
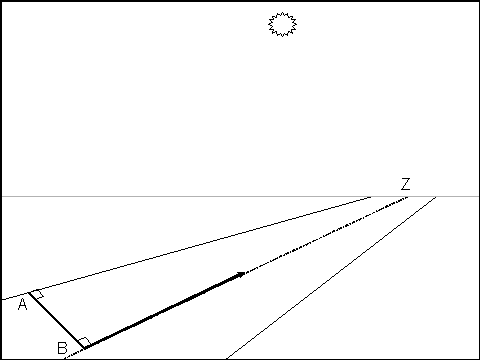
Let B represent any point along the centerline of the stream and Z the point of intersection of the horizon with the centerline of the stream. Then ray BZ runs along the centerline of the stream in the direction of streamflow. Given any point B, there exists a point A on the streambank such that AB is perpendicular to both the centerline of the stream and the streambank. Necessarily AB has a measure equal to half the width of the stream.
A ray originating at B and extending into space in the direction
of the sun is added in figure 2. The angular altitude of the sun
(relative to the plane of the stream surface) is labeled ![]() ,
and is calculated with the following equation (Byram and Jemison
1943):
,
and is calculated with the following equation (Byram and Jemison
1943):
(1) sin(
) = cos(
)sin(h)cos(
) + sin(
)sin(
)
Where ![]() is
the solar declination of the sun, h is the hour angle of the sun,
and
is
the solar declination of the sun, h is the hour angle of the sun,
and ![]() is the
latitude of the stream. Hour angle is a measure of "solar time";
the sun is in the plane of the equator at solar 6am and 6pm, and
perpendicular to the plane of the equator at solar noon and midnight.
is the
latitude of the stream. Hour angle is a measure of "solar time";
the sun is in the plane of the equator at solar 6am and 6pm, and
perpendicular to the plane of the equator at solar noon and midnight.
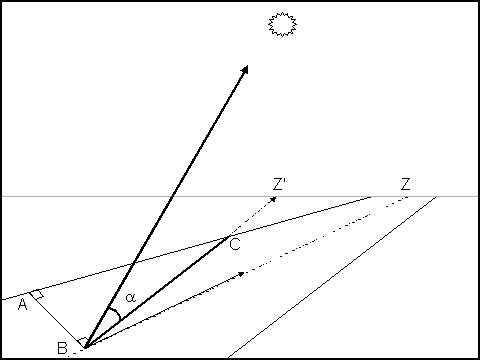
Let Z' represent a point on the horizon directly beneath the sun at any time of day (hour angle). Then ray BZ' has an angular measure which is the apparent azimuth of the sun at that time of day. This angular measure is calculated with the following equation:
(2)
cos(BZ') = [cos(![]() )cos(h)]
/ cos(
)cos(h)]
/ cos(![]() )
)
Figure 3 illustrates a quadrant defined by ABZ (assuming the streambank
and streamcenter lines remain parallel out to the horizon); where
BZ (i.e. stream azimuth) determines the orientation of the quadrant.
BZ' bisects the quadrant, and defines ![]() ,
calculated with the following formula:
,
calculated with the following formula:
(3)
![]() = 90°
- |{[BZ ± (K * 90°)] - BZ'}|
= 90°
- |{[BZ ± (K * 90°)] - BZ'}|
where K is equal to -1, 0, or 1. The choice of K and ± in
(3) is determined by the sun's azimuth relative to the stream's
azimuth. To simplify the calculation, ![]() is defined as the angle between the lines AB or A'B (the segment
ABA' extended in both directions) and the ray BZ'. Taking the absolute
value in (3) ensures that the angle is always positive and less
than 90°.
is defined as the angle between the lines AB or A'B (the segment
ABA' extended in both directions) and the ray BZ'. Taking the absolute
value in (3) ensures that the angle is always positive and less
than 90°.
Ray BZ' intersects the streambank at point C in Figure 3. This
creates triangle ![]() CAB,
which exists in the plane of the stream surface. By construction,
it is a right triangle containing
CAB,
which exists in the plane of the stream surface. By construction,
it is a right triangle containing ![]() solved for in (3).
solved for in (3).
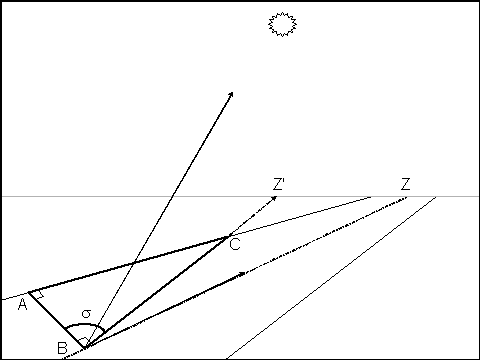
Since ![]() CAB
is a right triangle, then the following trigonometric identity holds:
CAB
is a right triangle, then the following trigonometric identity holds:
(4)
cos(![]() ) = AB
/ BC
) = AB
/ BC
Figure 3. Shade Model Construction Step 3: Ray BZ' intersects the plane of the interface between forest and stream at C. Since BZ
Since ![]() and
AB are known, (4) can be re-written and solved for BC:
and
AB are known, (4) can be re-written and solved for BC:
(5)
BC = AB / cos(![]() )
)
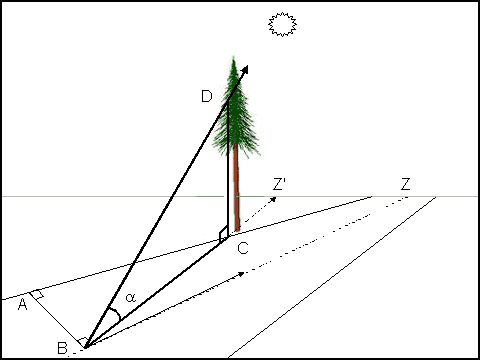
Figure 4 incorporates the solution to segment BC calculated in
(5) and the angular altitude of the sun (![]() )
calculated in (1). The ray originating at B extending towards the
sun (introduced in Figure 2) intersects the plane of the interface
between stream and buffer (i.e. the vertical plane of the streambank)
at D when BZ' intersects the plane at C. This results in the construction
of right triangle
)
calculated in (1). The ray originating at B extending towards the
sun (introduced in Figure 2) intersects the plane of the interface
between stream and buffer (i.e. the vertical plane of the streambank)
at D when BZ' intersects the plane at C. This results in the construction
of right triangle ![]() BCD
containing
BCD
containing ![]() .
The apparent height of the sun in the plane of the interface is
the measure of segment CD.
.
The apparent height of the sun in the plane of the interface is
the measure of segment CD.
As above, ![]() BCD
is a right triangle, and the following trigonometric identity must
hold:
BCD
is a right triangle, and the following trigonometric identity must
hold:
(6)
tan(![]() ) = CD
/ BC
) = CD
/ BC
Since ![]() and
BC are known, (6) can be re-written and solved for CD:
and
BC are known, (6) can be re-written and solved for CD:
(7)
CD = tan(![]() )
* [AB / cos(
)
* [AB / cos(![]() )]
)]
If we let W equal the width of the stream (which is known), then
AB = (W / 2). If we substitute this in (5) and substitute (5) for
BC in (7), we have the following:
(8)
CD = tan(![]() )
* {W / [2 * cos(
)
* {W / [2 * cos(![]() )]}
)]}
Figure 4. Shade Model Construction Step 4: The measure of BC was calculated in step 3,
Equation (8) reads that the height of the sun in the vertical plane
of the streambank is a function of angular solar altitude (itself
a function of hour angle, declination, and latitude), solar azimuth,
stream azimuth (which determines the orientation of quadrant ABZ
and therefore ![]() ),
and stream width.
),
and stream width.
The segment CD calculated in (8) defines the height at which direct solar rays are passing through the vertical plane of the streambank en route to the stream center.
To compute the canopy closure at this height, the crown area of each tree in the stand must be calculated. This calculation will involve two measurements commonly taken during a timber inventory ("cruising") or subsequently calculated by growth models: crown ratio (i.e. the proportion of the height of the tree that has foliage for primary production) and crown radius (i.e. the maximum distance from the bole to the end of a branch assumed to be at the base of the live crown).
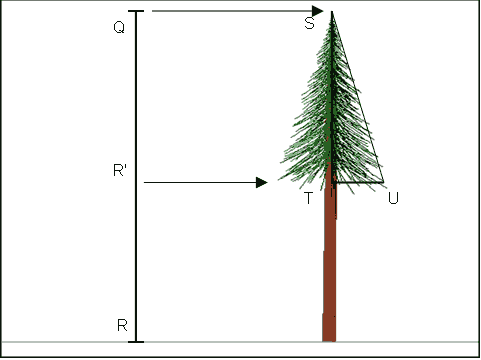
Figure 5 illustrates these measurements. Let segment QR represent the height of any given tree in the stand. Let segment QR' represent the length of the live crown on the tree. Then the ratio QR'/QR is the live crown ratio (LCR) for the tree. The length of the live crown - labeled ST in Figure 5 - is given in the following equation:
(9) Crown Length = Tree height * Live Crown Ratio
Or, symbolically as in Figure 5:
(10)
ST = QR * LCR
Figure 5. Shade Model Construction Step 5: The height of a given tree (QR), the crown ratio (not labeled), and maximum crown width (TU) are known from the inventory information, and the crown length (ST) can be calculated.
Segment TU in Figure 5 is the crown radius for the tree, which is also known (measured in the field or subsequently calculated automatically). The combination of segments ST with TU constructs the right triangle STU.
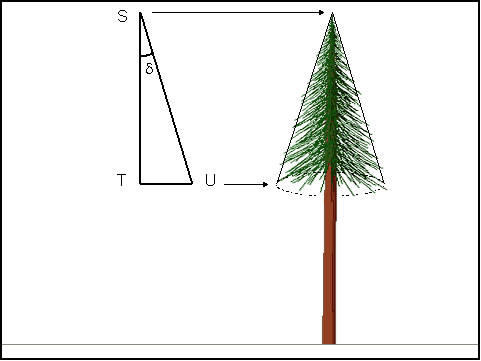
Figure 6 depicts a conic representation of the tree's crown that
is achieved by rotating ![]() STU
about the bole of the tree (on the ST axis). Figure 6 also illustrates
the apex angle of
STU
about the bole of the tree (on the ST axis). Figure 6 also illustrates
the apex angle of ![]() STU,
labeled
STU,
labeled ![]() . Since
. Since
![]() STU is
a right triangle,
STU is
a right triangle, ![]() can be calculated using the trigonometric identity for tangent:
can be calculated using the trigonometric identity for tangent:
(11)
tan(![]() ) = TU
/ ST,
) = TU
/ ST,
which, when solved for ![]() ,
becomes:
,
becomes:
(12)
![]() = arctan(TU
/ ST)
= arctan(TU
/ ST)
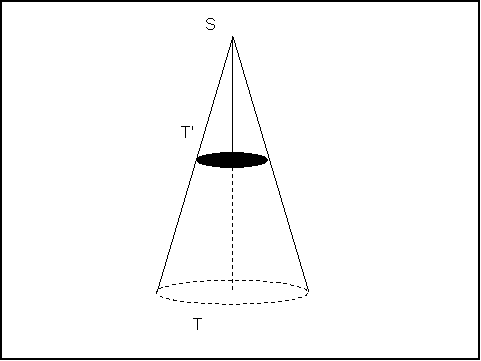
Figure 7 illustrates how ![]() allows for the calculation of cross-sectional area any point T'
along ST when ST' or T'T are given.
allows for the calculation of cross-sectional area any point T'
along ST when ST' or T'T are given.
When compared with some QR (Figure 5), CD (Figure 4) will be greater than, equal to, or less than QR.
For any tree in the stand, when CD is greater than QR or less than QR - ST, that tree will not contribute to canopy closure for that CD (it is assumed that the contribution of the tree stem to "canopy closure" [i.e., shade] is negligible). The only trees of concern are those where CD is within the live crown of the tree. Symbolically, this condition given by the equation:
(13) 0 <= (QR - CD) <= ST
Figure 6. Shade Model Construction Step 6: The measures of ST and TU were determined in Step 5. The shape of the crown can be represented by a conic section with apex angle
Since (13) is true, it is possible to substitute (13) for ST in (11) and solve for TU. The general form of the equation for finding the crown radius of a tree at CD:
(14)
TU = (QR - CD) * Tan(![]() )
)
and thus the crown area for any given tree such that (13) is true is given by the equation:
(15)
Crown Area = ![]() * [(QR - CD) * Tan(
* [(QR - CD) * Tan(![]() )]2
)]2
Figure 8 illustrates how a given CD results in various cross-sectional crown areas among trees in the stand. Note also that not every tree will contribute to crown area (and therefore crown closure) at that height class.
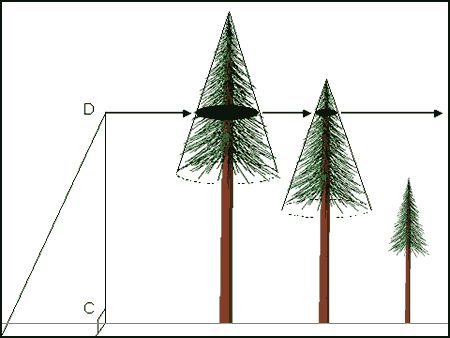
The sum of all applicable crown areas (at some CD) divided by the area of the riparian forest is the estimation of proportion of crown closure provided by the trees in the riparian zone.
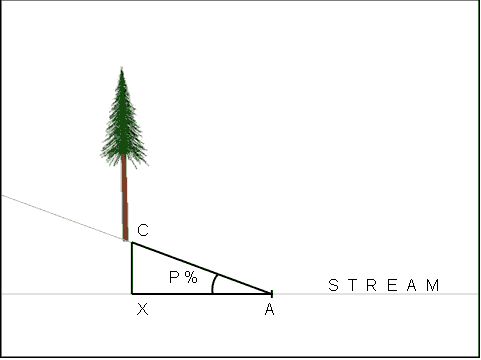
Figure 9 illustrates the effect of buffer slope in providing "topographic
shading." For a point A on the streambank of a given slope
of P%, the effective height of the buffer at some distance X from
A is the measure of the segment XC. Note that C is not located in
the streambank as previously, but in the buffer; this is because
the effect of slope at the streambank is zero. XA lies in the plane
of the stream surface, and XC is perpendicular to the plane; these
segments define the legs of the right triangle ![]() CXA.
The following formula provides the general solution for a slope
of P%:
CXA.
The following formula provides the general solution for a slope
of P%:
(16)
(XC / XA) * 100 = P%
Figure 8. Shade Model Construction Step 8: For a desired height in the plane of the interface (Step 4), the total cross-sectional area of all applicable trees can be calculated.
Figure 9. Shade Model Supplement 1: The vertical distance (XC) given a buffer slope (P%) at a desired distance (AX) from the plane of the interface between forest and stream can be calculated.
![]() CXA
is a right triangle, and therefore (16) can be re-written using
the trigonometric identity for tangent as:
CXA
is a right triangle, and therefore (16) can be re-written using
the trigonometric identity for tangent as:
(17) XC / XA = tan(P% / 100)
When solved for XC, (17) becomes:
(18) XC = XA * tan(P% / 100)
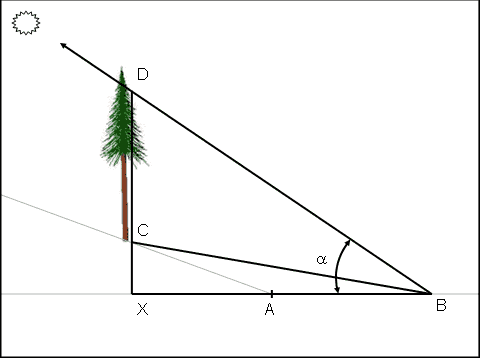
XC is a systematic increase in the heights of all trees X feet from the streambank (specifically, A). The effect of XC increases with X. This is illustrated in figure 10, which shows how the calculation of CD from (8) is modified to XD. X can represent any distance (e.g., the midpoint of the buffer when trees are assumed to be placed randomly within the buffer).
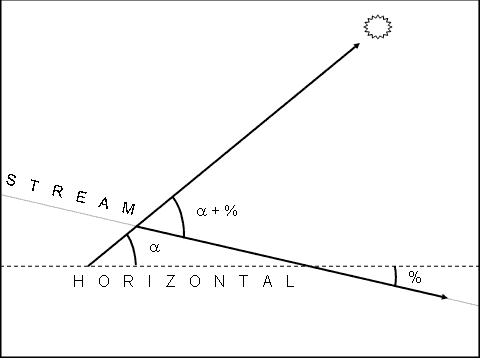
The effect of stream gradient is to alter the angular altitude
of the sun (![]() )
relative to the plane of the stream surface. Figure 11 illustrates
how a measurable stream gradient affects
)
relative to the plane of the stream surface. Figure 11 illustrates
how a measurable stream gradient affects ![]() .
The magnitude of the change is equal to the measure of the gradient.
The effect of gradient is positive when the sun's azimuth is ±
90 degrees to the azimuth of the stream (as in Figure 11). When
the sun's azimuth is outside this range, the effect will be negative.
Also, there is a difference in units between sun angle (radians)
and stream gradient (percent). The following equations convert from
percent to radian measures and vise-versa:
.
The magnitude of the change is equal to the measure of the gradient.
The effect of gradient is positive when the sun's azimuth is ±
90 degrees to the azimuth of the stream (as in Figure 11). When
the sun's azimuth is outside this range, the effect will be negative.
Also, there is a difference in units between sun angle (radians)
and stream gradient (percent). The following equations convert from
percent to radian measures and vise-versa:
(19) degrees = arctan(percent / 100),
(19')
radians = arctan(percent / 100) * (![]() / 180).
/ 180).
Figure 10. Shade Model Supplement 2: The effect of buffer slope is to increase the heights of trees in the riparian forest systematically by the measure of XC, for a given distance AX, and slope (Step 9).
Figure 11. Shade Model Supplement 3: The effect of stream gradient (%) is to change the altitude of the sun relative to the surface of the stream. A cross-sectional view of the plane of the stream surface and the plane of the horizontal illustrate the effect of stream gradient.
Theoretical Construction: Large Woody Debris Recruitment
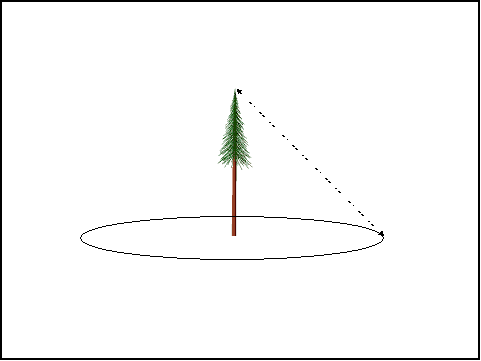
The probability space of a tree fall can be defined as a disk centered on a tree with radius equal to the tree's height; this is illustrated in Figure 12. The tree will fall somewhere within that disk. Initially we will assume that the probability distribution associated with the direction of a tree's fall is uniform across the disk. Thus the probability of a tree falling in any one direction is as likely as any other direction.
For any height class X in the riparian forest, we assume the horizontal
spatial distribution of X (i.e. the physical locations of tree stems
of all trees X feet tall) to be uniform across the buffer. Symbolically,
this property is expressed with the following equation:
(20)
Px(I,J) = Px(Q,R) ![]() (I,J),(Q,R)
(I,J),(Q,R)![]() B
B
Where P is the probability, (I,J) and (Q,R) are any two sets of spatial coordinates within the buffer, B.
The probability space for a tree fall is superimposed on a buffer in Figure 13. Figure 13 also illustrates that not every tree in the buffer has a positive probability of LWD recruitment. For all trees in a given height class X, only the subset of trees whose probability space for tree fall overlaps the stream have positive recruitment probabilities. Throughout the construction, this subset will be referred to as the set of LWD "candidates."
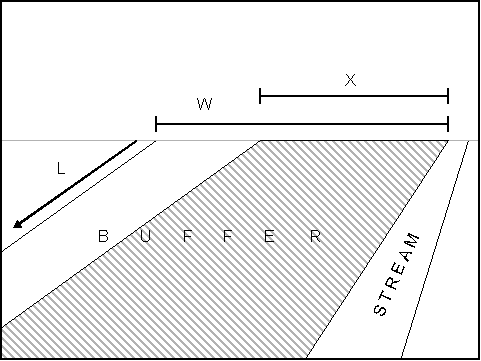
Let Nx represent the total number trees X feet tall in a buffer with length = l and width = w. Since the spatial distribution of trees in set Nx across the buffer is uniform (by assumption), the
Figure 12. LWD Model Construction Step 1: The probability space of a tree fall is defined as the circle centered upon the tree with radius equal to the height of the tree.
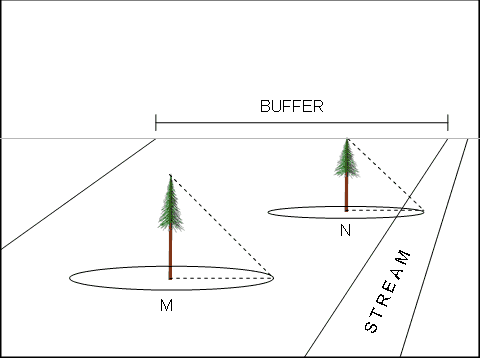
Figure 13. LWD Model Construction Step 2: The subset of trees in the riparian forest that can be considered "candidates" for LWD recruitment are those whose probability space for location of fall overlaps the stream. In the diagram above, tree M would not be a candidate; tree N would be a candidate.
subset of LWD candidates (nx) can be calculated with the following equation and is represented in Figure 14 (crosshatch represents the location of all candidates):
(21) nx = Nx * [(L * X) / (L * W)]
Therefore, the total number of LWD candidates in the riparian forest (nt) is the sum nx across all X in the forest:
(22) nt = n1 + n2 + n3 + ... + nx
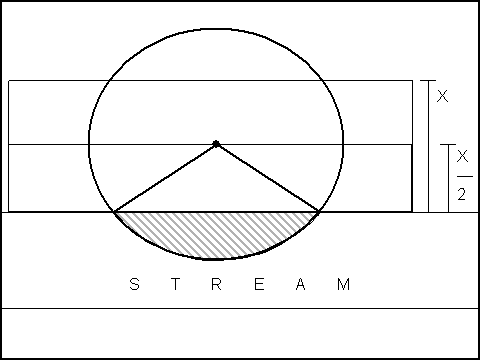
Necessarily, the expected distance (Ex) of the average candidate of height X is X/2 feet from the stream (a consequence of uniform distributions). This property is summarized with the following equation:
(23) Ex(Distance from stream) = X / 2
Combining nt from (22) with the result of (23), the probability of success (a tree-fall into the stream) can be calculated. The general scenario includes a candidate from height class X, which is expected to be X / 2 feet from the stream, and the probability space for the tree falling is superimposed. The probability of success illustrated in Figure 15 and is distinguished by gray crosshatch.
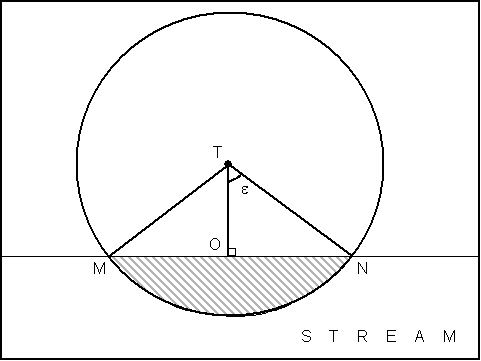
Figure 16 focuses on the sector of LWD recruitment success, defined
by segments TM and TN. Where T is the location of the tree at the
center of the probability space, and M and N are points of intersection
between the probability space and the streambank. The measures of
TM and TN are equal to the height class X.
Figure 14. LWD Model Construction Step 3: For a given height class (X), the proportion of the buffer containing candidates is X feet wide, represented by cross-hatch in the figure.
Figure 15. LWD Model Construction Step 4: For a given height class (X), candidates are distributed uniformly across the area of the buffer (or the corresponding proportion thereof). The expected distance of a candidate in the buffer is X/2 feet from the stream. The overlap discussed in Step 3 is represented with cross-hatch.
Figure 16. LWD Model Construction Step 5: For a given height class, segment TO is half the measure of the height class, while segments TM and TN are equal in measure to the height class (with M and N being points of intersection of the stream with the probability space for tree fall). The sector that represents the probability of success (cross-hatch) is defined by angle MTN. By construction, triangles
TO is half the measure of TM and TN, by (23). TO is also perpendicular
to MN, which is a segment along the streambank. Therefore, we have
by construction two congruent right triangles ![]() TOM
and
TOM
and ![]() TON.
Since
TON.
Since ![]() TOM
and
TOM
and ![]() TON
are congruent, then necessarily 2
TON
are congruent, then necessarily 2![]() =
= ![]() MTN.
MTN.
Since ![]() TOM
and
TOM
and ![]() TON
are right triangles and for any X, TM and TN are both equal to X,
and TO is equal to X / 2; then trigonometric identities will hold,
and we can solve for
TON
are right triangles and for any X, TM and TN are both equal to X,
and TO is equal to X / 2; then trigonometric identities will hold,
and we can solve for ![]() with the following equations:
with the following equations:
(24)
cos(![]() ) = (TO
/ TM) = (TO / TN)
) = (TO
/ TM) = (TO / TN)
Substituting X for TM or TN, and (X / 2) for TO, (24) can be rewritten as:
(25)
cos(![]() ) = (X
/ 2) / X
) = (X
/ 2) / X
(26)
cos(![]() ) = X
/ 2X
) = X
/ 2X
(27)
cos(![]() ) = 1/2
) = 1/2
(28) ![]() = arccos(1/2) = 60°
= arccos(1/2) = 60°
It becomes clear between (26) and (28) that ![]() is independent of X. For any height class X, the sector of success
is 2(
is independent of X. For any height class X, the sector of success
is 2(![]() ), which
is 2(60° ), or 120° . The probability of success for any
tree in any height class is given by the following equation:
), which
is 2(60° ), or 120° . The probability of success for any
tree in any height class is given by the following equation:
(29)
Ps = (120 / 360) = ![]()
Since we defined only two possible outcomes, success and failure,
the probability of LWD recruitment success is a binomial probability
with P(success) = ![]() and P(failure) =
and P(failure) = ![]() .
.
Given ntot candidates with probability of success independent of height class, the probability of some number, i, successes out of ntot candidates is computed with the following formula:
(30)
Pi = C(ntot,i) * (![]() ^ i)* (
^ i)* (![]() ^ ntot-i),
^ ntot-i),
where C(ntot,i) is the number of combinations possible from ntot items taken i at a time without repetition. This is called the binomial coefficient with parameters (ntot,i). The expected number of successes for a binomial event with ntot candidates, and a probability of success P, can be calculated with the following equation:
(31) E(successes) = ntot * p
Test Procedures: Shade Production
To test the model for reasonableness and sensitivity to change (relative
to an arbitrary set of initial conditions), multiple minute-by-minute
analyses (6am to 6pm solar time) were performed. Each analysis was
designed to measure the response of the model when the value of
a single variable is toggled greater than and less than the initial
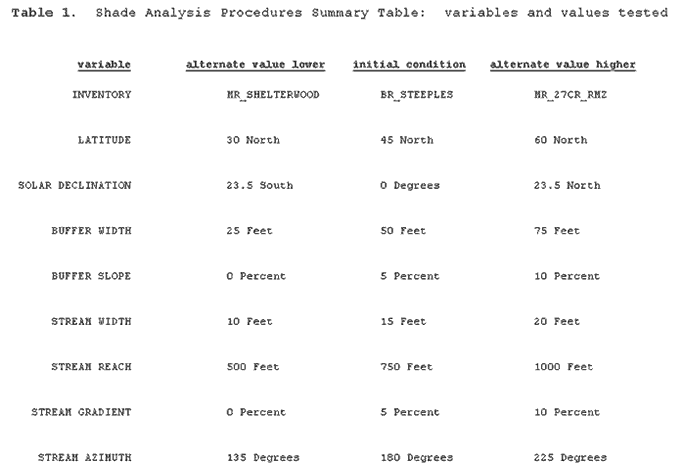
value (while all other variables remain constant). Table 1 lists
the model's variables and summarizes the values that each variable
held for a given analysis.
First, an arbitrary set of initial conditions was applied to the model and a minute-by-minute analysis was performed; establishing the baseline shade scenario. The set of initial conditions include:
(1) Forest Inventory: BR_Steeples
(2) Latitude = 45 degrees North
(3) Declination = 0 degrees (March 21st, Spring Equinox)
(4) Width of left buffer = 50 feet
(5) Width of right buffer = 50 feet
(6) Slope of left buffer to stream = 5 percent
(7) Slope of right buffer to stream = 5 percent
(8) Stream width = 15 feet
(9) Stream reach = 750 feet
(10) Stream gradient = 5 percent
(11) Stream azimuth = 180 degrees (due South)
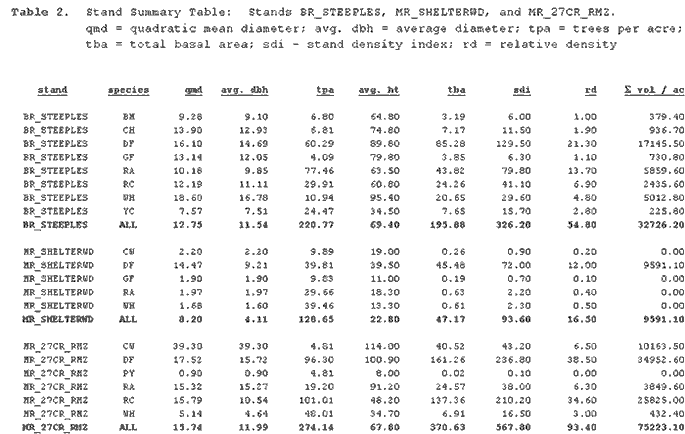
The initial forest inventory was BR_STEEPLES (a stand at the University
of Washington's Pack Forest). Analyses were also performed with
alternate inventories of MR_SHELTERWD and MR_27CR_RMZ. Table 2 contains
summary statistics for the stands.
Figures 17, 18, and 19 represent computer visualizations of MR_SHELTERWD,
BR_STEEPLES, and MR_27CR_RMZ, respectively.
The initial value for latitude was 45 degrees North (e.g. Salem,
Oregon). Additional analyses were performed with alternate latitudes
of 30 degrees North (e.g. Nogales, Arizona; on the U.S. / Mexico
border) and 60 degrees North (e.g. Anchorage, Alaska).
The initial value for solar declination (time of year) was 0 degrees (spring or fall equinox). Analyses were also performed with alternate declinations of 23.5 degrees South (winter solstice) and 23.5 degrees North (summer solstice).
The initial value for buffer width was 50 feet. Analyses were also performed with alternate buffer widths of 25 feet and 75 feet.
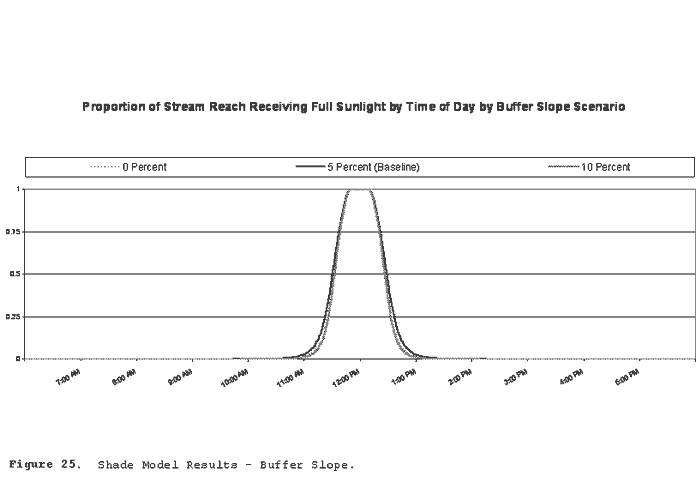
The initial value for buffer slope was 5 percent. Analyses were also performed with alternate slopes of 0 percent and 10 percent.
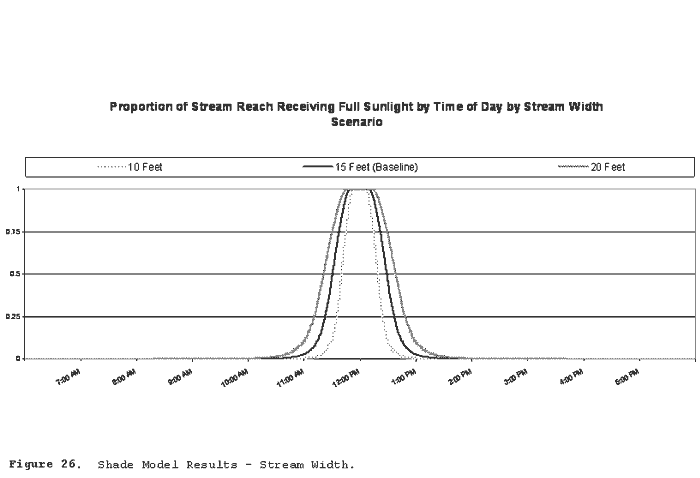
The initial value for stream width was 15 feet. Analyses were also performed with alternate stream widths of 10 feet and 20 feet.
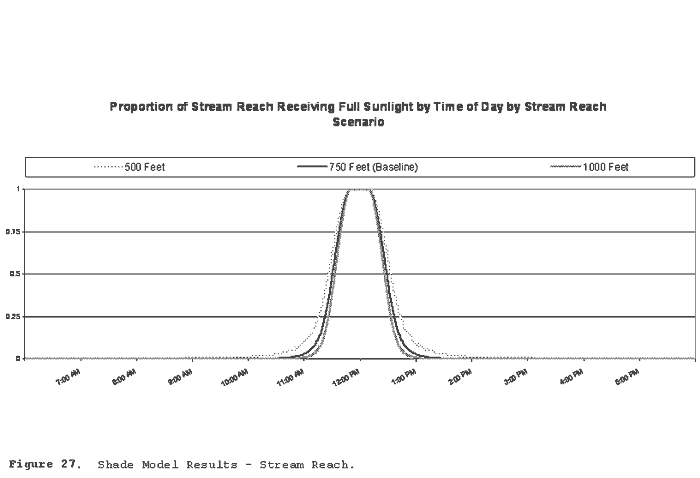
The initial value for stream reach (length) was 750 feet. Analyses were also performed with alternate reaches 500 feet and 1000 feet.
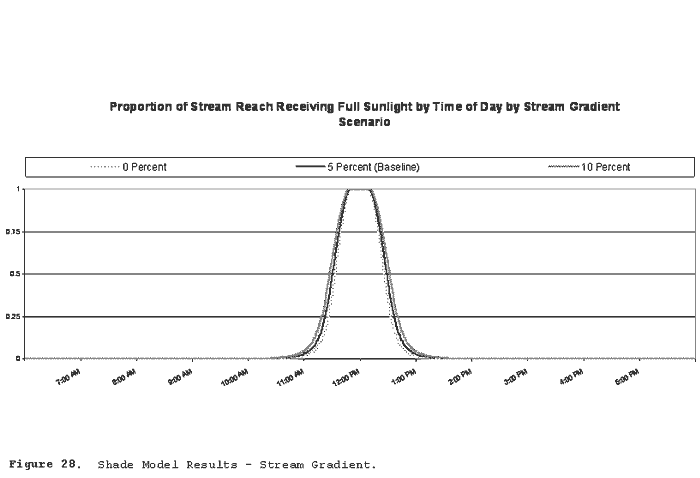
The initial value for stream gradient was 5 percent. Analyses were
also performed with alternate gradients of 0 percent and 10 percent.
Figure 17. Stand Visualization - MR_SHELTERWD.
Figure 18. Stand Visualization - BR_STEEPLES.
Figure 19. Stand Visualization - MR_27CR_RMZ.
The initial value for stream azimuth was 180 degrees (due South). Analyses were also performed with alternate azimuths of 135 degrees (South-East) and 225 degrees (South-West).
Test Procedures: Large Woody Debris
The large woody debris recruitment model constructed previously
was applied to the inventories for stands BR_STEEPLES, MR_SHELTERWD,
and MR_27CR_RMZ in the following manner: For a 750 foot reach, the
expected number of recruitments was calculated for buffers with
widths from 10 feet to 200 feet in 10 foot increments. From this,
both the marginal and cumulative expected number of recruitments
can be calculated for each additional 10 feet of buffer.
Test Results: Shade Production
Test results represent the proportion of stream reach where
the stream-center is receiving full, unfettered sunlight at a given
time of day (one minute intervals from 6am to 6pm, solar time).
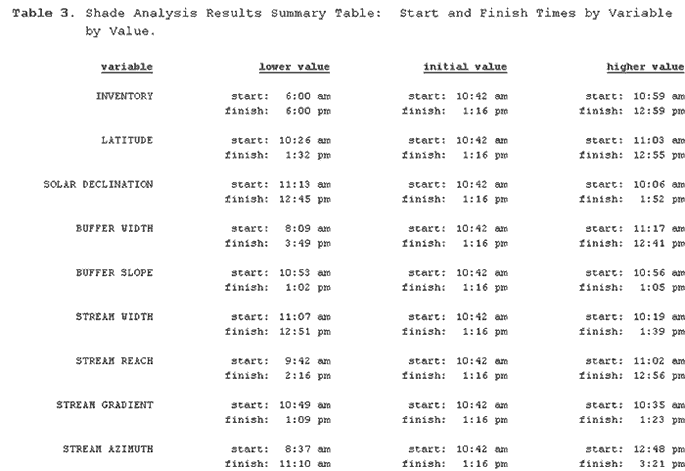
Table 3 lists each variable and the "start" and "finish"
time for each analysis. "Start" times correspond to the
first minute at which exposures are equal to or greater than one
percent; "finish" correspond to the last minute that exposure
is greater than one percent.
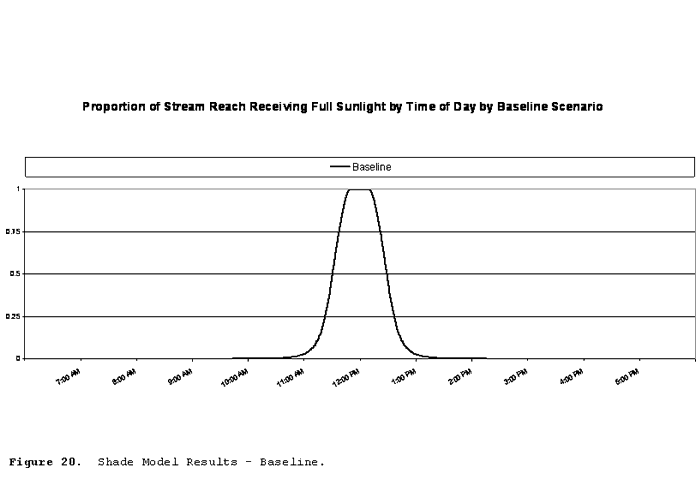
Figure 20 illustrates solar exposure by time of day under set of initial conditions specified in the test procedures section. This scenario will be referred to as the "baseline" scenario.
Figure 21 illustrates solar exposure by time of day under alternate forest inventory conditions. MR_SHELTERWD is the least dense inventory (Figure 17); BR_STEEPLES is the baseline inventory (Figure 18); MR_27CR_RMZ is the densest inventory (Figure 19).
Figure 22 illustrates solar exposure by time of day under alternate latitude conditions. 30 degrees North latitude corresponds to a stream near Nogales, Arizona, on the U.S./Mexico border. A stream at 45 North (baseline scenario) is near Salem, Oregon. 60 North is near Anchorage, Alaska.
Figure 23 illustrates solar exposure by time of day under alternate declination conditions. Declination was set to conditions simulating December 22nd (winter solstice), March 21st (spring equinox; baseline scenario), and June 21st (summer solstice).
Figure 24 illustrates solar exposure by time of day under alternate buffer width conditions. Buffer widths were set to 25 feet, 50 feet (baseline scenario), and 75 feet.
Figure 25 illustrates solar exposure by time of day under alternate buffer slope conditions. Buffer slopes were set to 0 percent, 5 percent (baseline scenario), and 75 feet.
Figure 26 illustrates solar exposure by time of day under alternate stream width conditions. Stream widths were set to 10 feet, 15 feet (baseline scenario), and 20 feet.
Figure 27 illustrates solar exposure by time of day under alternate stream reach conditions. Stream reach varied between 500 feet, 750 feet (baseline scenario), and 1000 feet.
Figure 28 illustrates solar exposure by time of day under alternate stream gradient conditions. Stream gradient was set to 0 percent, 5 percent (baseline scenario), and 10 percent.
Figure 29 illustrates solar exposure by time of day under
alternate stream azimuth conditions. Stream azimuth was set to 135
degrees (South-East), 180 degrees (due South; baseline scenario),
and 225 degrees (South-West).
Test Results: Large Woody Debris
Test results represent the expected number of recruitments from
a buffer with well defined dimensions and inventory composition.
Table 4 lists the expected number of recruitments from buffers with
750 feet of reach and various widths, under three alternate inventory
conditions (MR_SHELTERWD, BR_STEEPLES, MR_27CR_RMZ).
Figure 30 illustrates the expected number of marginal and cumulative recruitments for a stream with 750 feet of reach at widths from 10 feet to 200 feet (by 10 foot increments), under MR_SHELTERWD inventory conditions.
Figure 31 illustrates the expected number of marginal and cumulative recruitments for a stream with 750 feet of reach at widths from 10 feet to 200 feet (by 10 foot increments), under BR_STEEPLES inventory conditions.
Figure 32 illustrates the expected number of marginal and
cumulative recruitments for a stream with 750 feet of reach at widths
from 10 feet to 200 feet (by 10 foot increments), under MR_27CR_RMZ
inventory conditions.
Discussion and Conclusions: Shade
Production
Incident solar radiation will be transmitted, reflected, or absorbed.
Riparian forests play a critical role in moderating how much radiation
is transmitted to adjacent streams by both reflecting and absorbing
some of this radiation. Shade production by riparian forests is
an important factor in creating and maintaining habitat in adjacent
streams. Understanding the effect of various harvest intensities
(i.e. alternative management scenarios) on shade production is a
critical piece of information for managers and policy-makers.
The product of this research project - a mathematical model of this process - is the next step in providing this information. A deterministic model (i.e. a model where experimental conditions determine the outcome) such as this one allows managers to evaluate and compare the effects of various management scenarios on shade production prior to their implementation.
Results of the sensitivity analyses suggest that the model is constructed properly; it responds to changes as would be expected. Solar exposures are protracted at lower latitudes, at solar declinations closest to the summer solstice (+23.5 degrees), wider streams, steeper stream gradients on south-flowing streams, and at minimal buffer slopes. Conversely, solar exposures are contracted under opposite conditions.
The effect of buffer slope on shade production has significant
implications on riparian management prescriptions. Figures 9 and
10 illustrate how topographic shading effectively adds height to
the stand. For a given solar altitude (![]() ),
any positive buffer slope will increase the height CD as in Figure
4. While managers cannot affect the slope of a buffer through management,
they can affect the top height of the stand. Taller trees next to
a stream mean that the sun must achieve a greater angular altitude
in order to escape the reflective and absorptive effects of the
canopy. A metric useful in analyzing and comparing the relative
influence of riparian canopy on shade production is the ratio of
stand height to stream width. A higher ratio indicates a greater
effect of riparian forest on shade production. Such analyses are
important, but beyond the scope of this research.
),
any positive buffer slope will increase the height CD as in Figure
4. While managers cannot affect the slope of a buffer through management,
they can affect the top height of the stand. Taller trees next to
a stream mean that the sun must achieve a greater angular altitude
in order to escape the reflective and absorptive effects of the
canopy. A metric useful in analyzing and comparing the relative
influence of riparian canopy on shade production is the ratio of
stand height to stream width. A higher ratio indicates a greater
effect of riparian forest on shade production. Such analyses are
important, but beyond the scope of this research.
Managing for height is also important at lower latitudes. The lower
the latitude, the higher the maximum solar angle (![]() )
achieved each day. Therefore, a higher stand height is required
to achieve the same amount of shading as at higher latitudes.
)
achieved each day. Therefore, a higher stand height is required
to achieve the same amount of shading as at higher latitudes.
The results of testing the model under alternate management scenarios indicate that harvest intensity does have an effect on shade production. Studies suggest (Reifsnyder and Lull, 1965) that a closed canopy absorbs (and transmits) all long wavelengths (heat) of incident radiation; that is, a closed canopy approximates a "black body" for long wavelengths. Therefore, the forest has a significant effect on reflecting short-wave radiation (shade). A closed canopy can be considered a stand with 100 percent canopy closure. Consequently, a lower bound exists above which silvicultural treatments (or lack thereof) do not create more effective shade. A stronger argument is offered by (Adams and Sullivan 1989, Ice 2001, Waring and Schlesinger 1985), who concluded that any diffuse radiation (e.g. radiation passing through a forest canopy) has no capacity to directly affect stream temperature. Thus, the only aspect of the inventory information that is important to the accuracy of this model is the height of the stand; as any radiation passing through the canopy is irrelevant.
It must be stressed that inferences and predictions about amounts of stream temperature changes based on the results of this model cannot be made. As previously stated, stream temperatures are dependent not just on direct solar insolation (light) but on such factors as ambient air temperature, groundwater influx, substrate composition, discharge rate, and channel morphology. Although studies show that direct solar radiation is a principal cause of stream temperature deviation from its mean, no reliable conclusions can be made when considering light alone. Estimates of stream temperature can be made with additional analyses using the outputs from this model in conjunction with appropriate measurements of the variables listed above.
The necessary next step is to test the model in the field, so that deficiencies can be identified, and proper changes (or calibrations) can be made. If the model is determined to be satisfactory for the purposes of comparing effects between management scenarios (as opposed to predicting exposures at precise times accurately), then proper use of the model will require expertise of forest managers (to prepare a management plan and gather the predicted consequences of a chosen alternatives), fish biologists, stream ecologists, and hydrologists to determine the effect of the change in solar exposure on the continued production and maintenance of adequate aquatic habitat.
Development of tables showing the effects of sustained direct sunlight
on streams partitioned by variables such as discharge rate, width,
depth, substrate composition, and groundwater influx rate would
allow this model to make crude predictions of temperature changes
based on changes in harvest intensity and therefore sunlight.
Discussion and Conclusions: Large Woody Debris
Large woody debris recruitment is a binomial event: when a tree falls, it will either hit the stream (success) or it will not (failure). Large woody debris recruitment is an important event for production and maintenance of aquatic habitats. Only trees whose distance from the stream does not exceed their height are potential "candidates" for recruitment. Understanding the effect of silviculture on the set of candidates over time will allow managers and policy-makers to craft guidelines that ensure the viability of aquatic habitat now and in the future.
In contrast to the shade model discussed above, the experimental conditions do not determine the outcome in the LWD recruitment model; rather, the probabilistic behavior (a distribution) of the outcome. While the effects of various management scenarios can be evaluated and compared, the results are only a prediction of a probabilistic event, and cannot be expected to be matched in the field.
If the physical location of trees of a given height are distributed randomly (uniformly) across a buffer and there are no systematic influences on the direction of a tree fall, then the binomial probability of success is 1/3. This is the proportion of overlap of probability space on stream channel for the average tree. However, when there are systematic influences, the binomial probability of success can be adjusted accordingly.
Studies suggest that tree fall direction is not random. Van Sickle and Gregory (1990) suggested that the direction of a tree-fall is normally distributed with the mean direction being perpendicular to the stream channel. Unpublished data by Beschta (referenced in Robison and Beschta 1990) suggest that on hillslopes of 17 percent to 70 percent the probability of a tree falling downhill is 75 percent. If factors which positively or negatively affect the probability of recruitment can be quantified, then the probability of success can be tailored for site specific factors (e.g. slope, windthrow susceptibility, bank erosion and other mass-wasting events, buffers vs. unharvested conditions).
The results of the model constructed in this project illustrate that marginal recruitment (i.e. the increase in the expected number of recruitments for each additional 10 feet of buffer) diminishes as distance from the stream increases. This conclusion is supported in the entirety of the literature. The results from this test of the model also support the assertion (based on empirical analyses) of Fetherston, Naiman, and Bilby (1995) that 70% to 90% of the recruitments come from within the first 30 meters (~100 feet) from the streambank.
Figures 13 and 14 illustrate the recruitment probabilities for an individual tree and for all trees of a given height class. Clearly, a taller the tree results in a greater probability of recruitment. If there are more trees in taller height classes, then a greater proportion of the buffer can contain candidates (Figure 4). If there is a minimum level of recruitment potential required to maintain suitable habitat, taller trees will allow for greater flexibility in management prescription.
The quality of recruitments may be as important as the quantity of recruitments. That is, there may be differences in the effectiveness of LWD between root-wads and stumps and tree tops with lots of foliage. A useful metric to describe the effectiveness of LWD recruitments might be volume of LWD recruited. This would better illustrate the composition of the large woody debris. Such analysis is important, but beyond the scope of this thesis.
This model predicts the recruitment potential of a stand, not the predicted number of recruitments within an arbitrary temporal period. Conceptually, recruitment potential is the expected number of recruitments should all of the trees in the stand fall at the same time (and according to the probability distribution defined). Although it is unlikely that all trees will fall simultaneously, recruitment potential allows for comparisons among stands in any structural or seral stage. The structure of tree heights within a stand will change within growing seasons and between growing seasons; thus number and location of trees in any height class is dynamic. Therefore, the accuracy of predictions about recruitment potential are tied to the accuracy of the growth models. If however, this models is used primarily to compare the relative recruitment potential between various management alternatives, then accuracy is less important when compared to the model's precision. The precision of the model refers to the definitions and rules the model follows; assumptions of distributions, and how well it accounts for the systematic influences discussed above.
Applications to Management
Overall, it is important to note that any model, no matter how accurate, is not a decision making tool by itself. Models are decision-support tools to be used in creating a management plan for a set of objectives. These models do not determine the appropriate levels of shade production and large woody debris recruitment; they allow managers to assess the impact of various management scenarios (each with their own costs and benefits) on shade production and LWD recruitment.
The results of this research indicate that managing buffers for maximum height yields managers the most control of shade production and recruitment potential. Although the more shade and higher recruitment potentials may not lead to the better habitat conditions, managing for them allow managers the discretion to create flexible, perhaps non-traditional management plans that achieve similar results in terms of shade and LWD recruitment while gaining benefits (or mitigating costs) in other areas.
Bibliography
Adams, T.A., and Sullivan, K. 1990. The Physics of forest stream
heating: a simple model. Timber-Fish-Wildlife
Report No.
TFW-WQ3-90-007, Washington Department
of Natural Resources,
Olympia, Washington.
Barton, D.R., Taylor, W.D., and Biette, R.M. 1985. Dimensions of
riparian buffer strips required to
maintain trout habitat in
southern Ontario streams. North American
Journal of
Fisheries Management. 5:364-378.
Beechie, T.J., and Sibley, T.H. 1997. Relationships between
channel characteristics, woody debris,
and fish habitat in
northwestern Washington streams.
Transactions of the
American fisheries society. 126:217-229.
Beschta, R.L., Bilby, R.E., Brown, G.W., Holtby, L.B., and
Hofstra, T.D. 1987. Stream temperature
and aquatic habitat:
fisheries and forestry interactions.
In: Salo, E.O, and
Cundy, T.W. (eds.). Streamside management:
forestry and
fisheries interactions. University
of Washington, Institute
of Forest Resources, Contribution
No. 57. Seattle, Washington
Bisson, P.A. and 8 others. 1987. Large woody debris in forested
streams in the Pacific Northwest:
past present, and future.
In: Salo, E.O, and Cundy, T.W. (eds.).
Streamside
management: forestry and fisheries
interactions. University
of Washington, Institute of Forest
Resources, Contribution
No. 57. Seattle, Washington.
Brazier, J.R., and Brown, G.W. 1973. Buffer strips for stream
temperature control. Research Paper
No. 15, Forest Research
Laboratory, Oregon State University,
Corvallis, Oregon.
9 pp.
Brett, J.R. 1956. Some principals in the thermal requirements of
fishes. Quarterly Review of Biology.
31(2):75-87.
Brown, G.W. 1969. Predicting temperatures of small streams.
Water Resources Research. 5(1):68-75.
Brown, G.W., and Krygier, J.T. 1970. Effects of clear cutting on
stream temperature. Water Resources
Research. 6:1133-1139.
Bryant, M.D. 1983. The role and management of woody debris in
west coast salmonid nursery streams.
North American Journal
of fisheries management. 3:322-330.
Byram, G.M., and Jemison, G.M. 1943. Solar Radiation and Forest
Fuel Moisture. Journal of Agricultural
Research. 67:
149-176.
Castelle, A.J., Johnson, A.W., and Conolly, C. 1994. Wetland and
stream buffer size requirements -
a review. Journal of
Environmental Quality. 23:878-882.
Crookston, N.L., and Stage, A.R. 1999. Percent canopy cover and
stand structure statistics from the
Forest Vegetation
Simulator. General Technical Report
RMRS-GTR_24. Rocky
Mountain Research Station, USDA Forest
Service, Fort Collins,
Colorado.
Erman, D.C., Newbold, J.D., and Roby, K.B. 1977. Evaluation of
streamside bufferstrips for protecting
aquatic organisms.
Technical Completion Report, Contribution
No. 165. California
Water Resources Center, University
of California, Davis,
California.
Ganey, J.L., and Block, W.M. 1994. A comparison of two
techniques for measuring canopy closure.
Western Journal of
Applied Forestry. 9(1):21-23.
Harmon, M.E. and 12 others (1988). Ecology of coarse woody
debris in temperature ecosystems.
Advances in ecological
research. 13:133-276.
Ice, G. 2000. How direct solar radiation and shade influences
temperature in forest streams and
relaxation of changes in
stream temperature. Cooperative Monitoring,
Evaluation and
Research (CMER) Workshop: Heat transfer
processes in
forested watersheds and their effects
on surface water
temperature. Lacey, Washington, February
2000.
Johnson, A.W., and Ryba, D. 1992. A literature review of
recommended buffer widths to maintain
various functions of
stream riparian areas. King County
Surface Water Management
Division, Seattle, Washington.
Kelly, D.G. 1994. Introduction to probability. Macmillan, New
York: 11-73, 406-433.
Meyer, P.G. 1965. Introductory probability and statistical
applications. Addison-Wesley, Reading
MA: 1-12.
Murphy, M.L., and Koski, K.V. 1989. input and depletion of woody
debris in Alaska streams and implications
for streamside
management. North American Journal
of Fisheries
Management. 9:427-436.
National Council for Air and Stream Improvement, Inc. (NCASI)
1999. Assessing effects of timber
harvest on riparian zone
features and functions for aquatic
and wildlife habitat.
Technical Bulletin No. 775. Research
Triangle Park, NC:
National Council for Air and Stream
Improvement, Inc.
National Council for Air and Stream Improvement, Inc. (NCASI)
2000. Riparian vegetation effectiveness.
Technical Bulletin
No. 799. Research Triangle Park,
NC: National Council for
Air and Stream Improvement, Inc.
Patton, D.R. 1973. A literature review of timber harvesting
effects on stream temperature. Research
Note RM-249. Rocky
Mountain Forest and Range Experimental
Station, USDA Forest
Service, Fort Collins, Colorado.
Robison, G.E., and Beschta, R.L. 1990. Identifying trees in
riparian areas that can provide coarse
woody debris to
streams. Forest Science. 36:790-801.
Spies, T.A., Franklin, J.F., and Thomas, T.B. 1988. Coarse woody
debris in Douglas-fir forests of
western Oregon and
Washington. Ecology. 69(6):1689-1702.
Sullivan, K., Tooley, J., Doughty, K., Caldwell, J.E., and
Knudsen, P. 1990. Evaluation of prediction
models and
characterization of stream temperature
regimes in Washington.
Timber/Fish/Wildlife Report No. TFW-WQ3-90-006.
Washington
Department of Natural Resources,
Olympia, Washington.
Swanson, F.J., Lienkaemper, W.L., and Sedell, J.R. 1976.
History, physical effects, and management
implications of
large organic debris in western Oregon
streams. General
Techical Report PNW-56. USDA Forest
Service, Pacific
Northwest forest and range experiment
station, Portland,
Oregon.
Swanson, F.J., and Lienkaemper, G.W. 1978. Physical consequences
of large organic debris in pacific
northwest streams.
General Technical Report PNW-69.
USDA Forest Service,
Pacific Northwest forest and range
experiment station,
Portland, Oregon.
Triska, F.J., and Cromack, K.J. 1979. The role of wood debris in
forests and streams. In: Forests:
Foresh perspective from
ecosystem analysis. Proceedings of
the 40th annual biology
colloquiam, Oregon State University
Press, Corvallis,
Oregon.
Van Sickle, J., and Gregory, S.V. 1990. Modeling inputs of large
woody debris to streams from falling
trees. Canadian Journal
of Forest Research. 20:1593-1601.