Chapter 1. Basic Wood Properties

Table of Content

Moisture Content

      Formulas

            •Moisture content on an oven-dry basis
            (MC_od)

            •Moisture content on a wet or original
              basis (MC_w)

      Conversion Between MC_od and MC_w   

      Fiber Saturation Point (fsp),  Shrinkage, and Swelling
 

            •Calculating shrinkage (Sh) percentage

            •Calculating swelling (Sw) percentage

      Typical Moisture Contents of Wood  

            •Equilibrium moisture content (EMC)

            •Kiln-dried products

            •Air-dried products

             •Green products

Density and Specific Gravity 

      Density

      Specific Gravity     

Calculating the Weight of Wood Products 

      Basic Calculations

(Go to calculation sheet to calculate weight; Go to calculation sheet to calculate volume)

      Simplifying the Calculations

Product Examples

      Logs              

      Cords   

      Lumber

      Plywood

       Veneer 

Chapter 1. Basic Wood Properties

        This chapter explains how moisture content, shrinkage, and specific gravity of wood are meas­ured and gives procedures for estimating weight density in pounds per cubic foot or kilograms per cubic meter of solid wood. Examples using informa­tion in the remaining chapters illustrate methods for estimating weight for various products.

Moisture Content

        Water is naturally present in all parts of a tree and permeates the wood structure. Water com­monly makes up more than half the weight of a living tree, a fresh log, or wet chips. The term green refers to this initial condition. However, when a tree dies or is harvested, bucked into logs, or pro­cessed into products, wood moisture content adjusts toward equilibrium with the temperature and humidity of its surroundings. It eventually reaches an equilibrium at which it still retains some mois­ture. The only case when wood contains no moisture is when it is kept in an oven above 100^oC. In this environment all water is eliminated and the wood is referred to as oven dried. In contrast, kiln drying is designed to bring wood to a moisture content similar to the environment expected in service. As the environment changes, wood will take on or lose moisture as it adjusts to these new conditions. These adjustments may be accompanied by shrinkage or swelling.

        To illustrate calculation of moisture content and other properties, consider a hypothetical piece of lumber 16 feet long with nominal thick- ness and width of 2 and 4 inches respectively. Assume that a researcher carefully measured its volume and weight when green, kiln-dry, and oven-dry, obtaining the following results:

Condition	Volume (ft3)	Weight (lb)
Green	0.78	40.0
Kiln-dry	0.73	22.3

Oven-dry

0.68

19.4

 

Formulas

        Wood moisture content may be expressed in either of two ways, hence it is important to know which is being used. Using the data above, the following formulas show how to find the percent­age of moisture on an oven-dry basis (MC_od) or on a wet or original basis (MC_w).

Moisture Content on an Oven-dry Basis (MC_od)

MC_od       =  100  _*  weight of water / oven-dry weight                   
                =  100  _*  (22.3  –  19.4)/19.4  = 15%   kiln-dry

                =  100  _*  (40.0  –  19.4)/19.4  = 106%   green

MC_od is commonly used in solid wood industries such as lumber and plywood. Note that on this basis, moisture content can exceed 100%.

Moisture Content on a Wet or Original Basis (MC_w)

MC_w =  100  _*  weight of water/original weight                                                        
=  100  _*  (22.3  –  19.4)/22.3  =  13%  kiln-dry
=  100  _*  (40.0  –  19.4)/40.0  =  52%   green

MC_w is commonly used in the pulp and paper and the wood energy industries. Note that on this basis, moisture content can never reach 100%.

Conversion Between MC_od and MC_w

MC_od =  100  _*  MC_w / (100  –   MC_w)
MC_w    =  100  _*  MC_od / (100  +   MC_od)

Fiber Saturation Point (fsp), Shrinkage, and Swelling

        When wood dries below a certain moisture content, referred to as the fiber saturation point (fsp), it begins to shrink and continues to do so until it is oven-dry. Conversely, wood that is below fsp will swell as it takes on moisture and this will continue until fsp is reached. Changes in moisture content above fsp have no effect on shrinkage and swelling. Fsp varies among species, but a value of 30% MC_od (23% MC _{style='font-size:9.0pt'>w}) is commonly assumed.

Table 1-1<.  Moisture content, shrinkage, and specific gravity of some western species.

Calculating Shrinkage (Sh) Percentage

        Sh  =  100  _*  decrease in size / original size. Here the "size" could be length, width, thickness, or overall volume, hence the formula can be used to calculate longitudinal shrinkage (Shl), volumetric shrinkage (Shv), or shrinkage in other directions. Table 1-1 presents shrinkage data for several western species and illustrates the variability between species and the differences due to grain direction in wood. In dealing with conversion factors, one is most often concerned with changes in volume, hence volumetric shrinkage values are of interest. Using the 2x4 data, total volumetric shrinkage (green to oven-dry) is

        Shv_t   = 100  _*  (0.78  –  0.68)/0.78  =  12.8%.

Similarly, volumetric shrinkage green to kiln-dry (15% MC_od) is

        Shv₁₅  =  100  _*  (0.78  –  0.73)/0.78  =  6.4%.

In the absence of actual measurement data, shrink­age from green to any intermediate moisture content, x, can be calculated by interpolation. Using volumetric shrinkage as an example

        Shv_x  =  Shv_{t  *}  (fsp  –  MC_{od, x})/fsp.

Assuming fsp is MC_od = 30%_, the volumetric shrinkage from green to kiln-dry (MC_od, x = 15) is

        Shv₁₅  =  12.8  _*  (30  –  15)/30  =  6.4%.

Calculating Swelling (Sw) Percentage

        Sw = 100  _*  increase in size / original size.

Suppose a contractor placed the kiln-dried 2x4 outdoors for several weeks during a rainy period and that it has returned to the green size. The percentage of swelling is

        Sw = 100  _*  (0.78  –  0.73)/0.73  =  6.8%.

This example illustrates that swelling and shrinkage percentages are not equal, since calculation of each is based on the starting dimension. Calculations for swelling in specific directions are similar.

Typical Moisture Contents of Wood

Equilibrium Moisture Content (EMC).     Wood ex­posed to air with a constant temperature and rela­tive humidity will eventually reach a constant moisture content called equilibrium moisture content (EMC). EMC normally reflects moisture content ex­pressed on an oven-dry basis. EMC varies with both humidity and temperature, with the former domin­ating. Changes in humidity and temperature cause wood products to move toward a new EMC level. The values listed below indicate the range of EMC that various products will reach at a temperature of 70^oF (21^oC) for relative humidities of 30 to 90% (Haygreen and Bowyer 1989).

Kiln-Dried Products.     Many wood products are dried during manufacture to a moisture content that approximates the EMC they will experience in their final use. This tends to minimize dimension changes due to shrinkage and swelling during use. By reducing weight, kiln drying may also reduce freight charges.

Air-Dried Products.     The moisture content of air-dried products in outdoor situations is variable because of the seasonal changes in the environment. However, a reasonable average would be approxi­mately 20% MC_od.

Green Products.     The moisture content of green or fresh wood as found in the living tree or logs is highly variable and depends on species, locale, season of the year, and heartwood and sapwood content of the wood. Table 1-1 presents green MC_od for some western species and illustrates the var­iation that can be encountered. Some products, especially lumber, are often sold in the green con­dition with the expectation that they will air-dry sufficiently before use. If this does not occur, diffi­culties with excessive shrinkage may result.

Density and Specific Gravity

Density

        Wood density is simply its weight per unit volume, hence this measure has units such as lb/ft³. Synonyms sometimes used are weight density and bulk density. For these to be meaningful, the mois­ture content at which the weight and volume were measured must be indicated; in some cases weight and volume are at the same moisture content while in other cases they are at different moisture contents.

        For example, the green weight of the 2x4 (40.0 lb) can be divided by its green volume (0.78 ft³), its kiln-dry volume (0.73 ft³), or its oven-dry volume (0.68 ft³), resulting in densities of 51.3, 54.8, and 58.8 lb/ft³, respectively. Example 1 lists these as the first row of values. The second row represents densities when the kiln-dry weight is divided by the three volume measures, and the bottom row represents densities when the oven-dry weight is used.

        In Example 1, the density 51.3 lb/ft³ would be useful for predicting the weight of green 2x4s that must be handled by labor and machinery in the sawmill. The density 34.9 lb/ft³ can be applied only to actual cubic lumber volumes measured after drying to 15% MC_od^; it would estimate the ship­ping weight of the dried lumber. The density 32.7 lb/ft³ could be used to predict the shipping weight of kiln-dried 2x4s from the cubic volume measured when the lumber is in the green condition. Each of the remaining six density values has a particular interpretation and application. This example illustrates that merely stating the units of weight and volume (i.e., lb/ft³) is am­biguous without further statement of the moisture content at which each of these measurements was taken. It should be obvious that there are an infinite number of weight densities and that weight density of wood varies continuously with moisture content, as shown by Figure 1-1. The kink in the curve is due to the effect of shrinkage on volume when moisture content is below fsp.

Figure 1-1. Effect of moisture content on density, SG_g = 0.40.

Specific Gravity

        Specific gravity is the density of wood relative to the density of water, and for this reason the terms relative density and basic density are sometimes used. Specific gravity is used as a basis to standardize comparisons among species and products. To reduce confusion from varying moisture content, specific gravity of wood is based on oven-dry weight and volume measured at one of the following MC_od conditions: 0% (oven-dry), 12%, or green. These will be referred to in this book as SG_od, SG₁₂, and SG_g. When referring to specific gravity, it is important to indicate which of these volume bases is used. SG₁₂ is often reported in the literature, because MC_od = 12% is a standard moisture content at which many wood properties are tested. SG_g is commonly reported due to the relative ease of measurement.

The volume and weight data presented for the 2x4  can be combined into nine densities (lb/ft³):

Volume basis
                                                                       

Example  2                  

Continuing the 2x4 example, and noting that water weighs 62.4 lb/ft³:

      SG_g    =  24.9 lb/ft³ / 62.4 lb/ft³  =  0.40.

      SG_od  =  28.5 lb/ft³ / 62.4 lb/ft³  =  0.46.

Example  3   

Calculate SG₁₅ for the 2x4. Previously, it was found that Shv₁₅  =  6.4%. Therefore

      SG₁₅  =   0.40/(1 – 6.4/100)   =   0.427  ~  0.43.

This value could also be calculated directly using the density from Example 1. The correct density to use is that with an oven-dry weight and volume taken when kiln-dry. Thus

      SG₁₅  =  26.6 / 62.4   =    0.426   ~  0.43.

The slight difference is due to rounding.

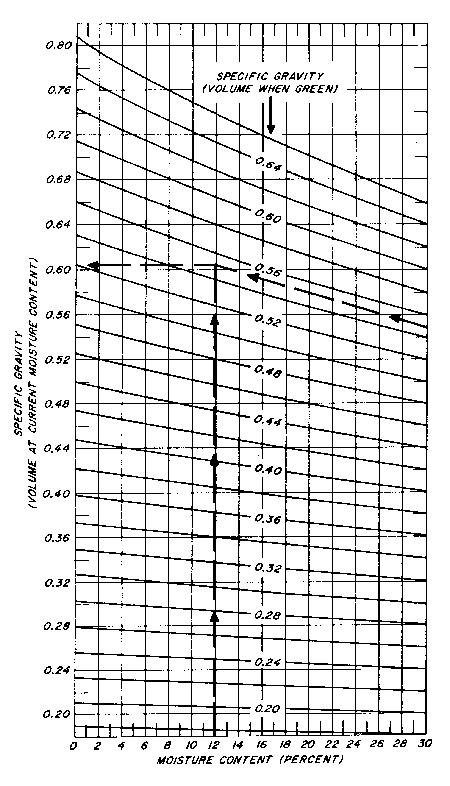
       Note in Example 2 that the units of measure cancel, so specific gravity is unitless. Also, note that specific gravity for this wood has risen from 0.40 to 0.46 as the volume basis changed from green to oven-dry. This is due to the effect of volumetric shrinkage below fsp. Above fsp, volume does not change; so specific gravity is the constant green basis value. Figure 1-2 plots specific gravity against MC_od. The kink corresponds to the onset of volumetric shrinkage below fsp. Table 1-1 pre­sents the average and range of SG_g for some western species.

Figure 1-2. Effect of moisture content on specific gravity, SG_g = 0.40.

Frequently, data on specific gravity at a particular moisture content basis may not be available. The following formula can be used to estimate SG at MC_od = x:

SG_x = SG_g /(1 – Shv_x/100)      0 ≤ x ≤fsp.

See Example 3.

Calculating the Weight of Wood Products

        The most accurate method for estimating weight is to weigh representative samples. In cases involving transportation, shippers often have weight tables that should be used. In situations where sampling is not possible and shipping tables are not available, the methods in this section can be used. The reader should be aware that wood is variable and an estimate based on published averages for a species may differ substantially from reality. For example, the author was involved in a request to estimate the weight of a large redcedar log. Since the dimensions were carefully measured, the estimate of cubic volume was regarded as reasonably accurate. But there was no information on the specific gravity or moisture content of this log. The estimated weight, based on redcedar averages shown in Table 1-1, was about one-third the actual weight later obtained on a truck scale. The log had either a higher average specific gravity, higher moisture content, or both.

Example  4  

A debarked log contains 44 ft³ of wood and it is desired to determine the load it will place on a conveyor. Assuming the SGg of the species involved is 0.40 and that the log has an MC_od of 60%, its weight is

      44 ft³ _* 0.40 _* 62.4 lb/ft³ _* (1 + 60/100) = 1,757 lb.

Since the log is in the green condition and specific gravity
is on a green volume basis, the units are consistent.

Example  5

Suppose instead that a pulp mill wished to estimate the weight of oven-dry fiber contained in the log of
Example 4.

      44 ft³ _* 0.40 _* 62.4 lb/ft³ _* (1 + 0/100) = 1,098 lb.

As in Example 4, the log volume is green, hence specific gravity on a green volume basis should be used.

Example  6

Suppose the log in the previous examples is processed into 2x4s as discussed earlier and that the recovery of dry (15% MC_od) 2x4s is 45% of the cubic volume of the log. Thus there is a stack of dried 2x4s which, if measured precisely, contain 0.45 _* 44 = 19.8 ft³. Referring to the weight calculation formula, the moisture content is known to be 15%. The specific gravity information available is SGg = 0.40 and SG_od = 0.46. However, what is needed is the specific gravity based on volume measured at 15% MC_od, which was found to be 0.43 in Example 3.The
weight of the kiln-dry 2x4s from this log is

     19.8 ft³ _* 0.43 _* 62.4 _* (1 + 15/100) = 611 lb.

Basic Calculations

        Assuming the moisture content and specific gravity are known, the weight of wood is calculated as follows:

        (density of H₂0)  _*  (1+ MC_od /100)

where "volume" is in cubic feet or cubic meters and the density of water is 62.4 lb/ft³ or 1,000 kg/m³. The specific gravity basis should correspond to the moisture content of the volume involved.

        SG_g is used in both Examples 4 and 5, but in Example 4 the last term includes the weight of water expected in a green log while the weight of water is excluded in Example 5. Remember that specific gravity was defined as always based on density expressed as oven-dry weight per unit volume.

(Go to calculation sheet to calculate weight; Go to calculation sheet to calculate volume)

Figure 1-3. Relation of specific gravity and moisture content. Source: USFS (1987).

Simplifying the Calculations         Figure 1-3 is the same as Figure 1-2 except there are lines for a range of SGg and the horizontal portion beyond fsp (30% MCod) has been elimin­ated.  Figure 1-3 provides a simple way to convert SGg to another basis. For example, to estimate SG15 for a species with SGg = 0.40, find 15% MCod on the bottom axis, move vertically to the curve for SGg = 0.40, and read approximately 0.43 from the left axis. A species having SGg = 0.55 has SG12 = 0.605, as shown by the bold arrows. A species with SGg = 0.40 has SGod = 0.45. This graph assumes an average volumetric shrinkage of North American spe­cies and that fsp = 30% MCod. While only approximate, it should be sufficient for most applications. Table 1-2 summarizes calculations to estimate weight density in lb/ft3 for combinations of specific gravity and MCod. If it is desired to convert table weights from lb/ft3 to kg/m3, multiply the table value by 16.0185 (Appendix 1).

Table 1-2  Density of Wood as a Function of Specific Gravity and Moisture Content (MC_od)

Moisture                                      Density in pounds per cubic food when the specific gravity is-

 content                                                                                                                                                                                                        

of wood                    0.30                     0.32                      0.34                  0.36                   0.38                  0.40                      0.42                      0.44                   0.46                  0.48

%

Moisture                            Density in pounds per cubic food when the specific gravity is-

 content                                                                                                                                                                                                                                                                                                               

of wood                   0.50                   0.52                   0.54                     0.56                  0.58                  0.60                   0.62                   0.64                       0.66                  0.68                   0.70

Pct

To get Kg/m³ multiply table entry by 16.0187.

Source: USFS (1987)

Product Examples

Logs

1.   Estimate the weight per MBF Scribner of the sample logs in Table 2-6.

Assumptions  (Douglas-fir):

Density  (Table 1-2):  56.2 lb/ft³ by interpolation

Log scale ratio (Table 2-6):

        4.30 BF/ft³ West-side

        5.93 BF/ft³ East-side

Weight/MBF West-side Scribner:

        (56.2 lb/ft³ ) / (4.30 BF/ft³) _* 1,000 BF/MBF =            13,070 lb/MBF.

Weight/MBF East-side Scribner:

        (56.2 lb/ft³) / (5.93 BF/ft³) _* 1,000 BF/MBF =             9,477 lb/MBF.

2.   To estimate the weight of oven-dry fiber/MBF, substitute a density of 28.1 oven-dry lb/green ft³.
This value is obtained at the intersection of SG = 0.45 and MC_od = 0 in Table 1-2.   

3.   Estimate the weight of a cunit of the sample logs in Table 2-6.

      From parts 1 and 2 above, a cubic foot weighs 56.2 lb green and 28.1 lb oven-dry. Multiplying these values by 100 ft³/cunit yields 5,620 lb green and 2,810 lb oven-dry.

4.   Gross versus net scale effect.  When estimating log weights, the difference between gross and net scale can be important. For example, suppose a log truck is found to have a load that weighs 100,000 lb and the gross and net scales are found to be 8,000 and 6,000 BF respectively. Division shows that the weight densities are 12,500 lb/MBF gross scale and 16,667 lb/MBF net scale.

Cords

1.   Estimate the weight of a cord of freshly cut and stacked red alder. From Table 1-1 alder has SG_g = 0.37 and MC_od = 97. Using interpolation, Table 1-2 yields a density of 46.1 lb/ft³. Assuming that a cord contains 85 ft³ solid wood, it weighs  85  _* 46.1 = 3,918 lb.

2.   Suppose this cord has been allowed to air dry (MC_od approximately 20%). Use Table 1-2 to find that the density is 27.7 lb/ft³, hence the cord weighs 85  _*  27.7 = 2,354 lb.

3.   A pulp mill wants to buy this cord but is willing to pay only for the oven-dry wood fiber (i.e., MC_od = 0%). Use Table 1-2 to find that the density is 23.1 lb/ft³, hence the dry fiber in the cord weighs 85  _*  23.1 = 1,964 lb.

Thus a truck driving across a scale would show that the fresh cord weighs almost 2 tons while the pulp mill wants to pay only for the wood fiber it contains (about 1 ton). This is why weight scaling factors are developed by pulp mills.

Lumber

Estimate the weight of 1,000 BF of Douglas-fir
S-Dry 2x4s.

Assumptions:  SG_g = 0.45, MC_od = 15%.

Figure 1-3, SG_g = 0.45 translates to SG₁₅ = 0.48.

Table 1-2 has a weight density (interpolated) of 34.4 lb/ft³ at the intersection of 15% MC and SG = 0.48.

Table 4-6 shows that the BFFR for S-Dry 2x4s is 18.29 BF/ft³.

The cubic feet represented by 1,000 BF of S-Dry 2x4s is obtained by dividing 1,000 by the BFFR, hence

        1,000 / 18.29 = 54.67 ft³ of S-Dry 2x4s.

Therefore, the weight of 1,000 BF is

        54.67 ft³  _*  34.4 lb/ft³ = 1,880 lb.

Plywood

Estimate the weight of 1,500 square feet of 1/2 inch Douglas-fir plywood.

Assumptions:  SG_g  =  0.45, MC_od = 8%.

Figure 1-3 translates SG_g = 0.45 to SG₈ = 0.49.

Table 1-2 has a weight density (interpolated) of 33.0 lb/ft³ at the intersection of 8% MC and SG  = 0.49.

Using the procedures in Chapter 5, 1,500 square feet of 1/2 inch plywood is equivalent to 62.5 ft³.

Therefore, the weight is

        33.0 lb/ft³ _* 62.5 ft³ = 2,062 lb.

The actual weight could be somewhat higher due to the additional weight of resin in the gluelines.

Veneer

Estimate the weight of nominal 1,000 square feet of 1/10 inch Douglas-fir green veneer.

Assumptions:  SG_g  = 0.45, MC_od  = 80%.

Since this is green veneer above fiber saturation point, no specific gravity translation is needed.

Table 1-2 has a weight density (interpolated) of 50.55 lb/ft³ at the intersection of 80% MC and SG = 0.45.

Using the procedures in Chapter 5, the volume in cubic feet is

        0.08333 _* 1,000 _* 1/10 = 8.33 ft³.

Since veneer volumes are normally stated on the basis of nominal sheet sizes, increase by 12% (Chapter 5) to get the total quantity of wood as
9.33 ft³.

The weight is

        50.55 lb/ft³ _* 9.33 ft³ = 472 lb.